
����Ŀ����1���������֣���ͼ�٣�С������һ������������ABC������AB=AC������ABC�����ֱ���AB��ACΪ��������������ֱ��������ABD��ACE���ֱ�ȡBD��CE��BC���е�M��N��G������GM��GN��С�������ˣ��߶�GM��GN��������ϵ��__________��λ�ù�ϵ��__________��
��2�����˼����
��ͼ�ڣ�С���ڴ˻����Ͻ���������˼�����ѵ���������ABC��Ϊһ�����������Σ�����AB��AC�������������䣬С�����ֵ��������ۻ���������˵�����ɣ�
��3���������
��ͼ�ۣ�С���ڣ�2���Ļ����ϣ������˽�һ����̽��������ABC���ڲ�ֱ�������ֱ��������ABD��ACE�������������䣬���ж���GMN����״��������֤����

���𰸡���1��MG=NG�� MG��NG����2��������MG=NG��MG��NG����3���𰸼�����
����������1������SAS�жϳ���ACD�ա�AEB���ó�CD=BE����ADC=��ABE�������жϳ���BDC+��DBH=90����������BHD=90�����������������λ�߶������ɵó����ۣ�
��2��ͬ��1���ķ������ɵó����ۣ�
��3��ͬ��1���ķ����ó�MG=NG�����������������λ�߶����͵����������ɵó����ۣ�
��1������BE��CD�ཻ��H����ͼ1��
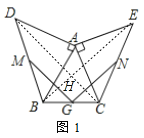
�ߡ�ABD����ACE���ǵ���ֱ�������Σ�
��AB=AD��AC=AE����BAD=��CAE=90��
���CAD=��BAE��
���ACD�ա�AEB��SAS����
��CD=BE����ADC=��ABE��
���BDC+��DBH=��BDC+��ABD+��ABE=��BDC+��ABD+��ADC=��ADB+��ABD=90�㣬
���BHD=90�㣬
��CD��BE��
����M��G�ֱ���BD��BC���е㣬
��MG��CD��MG=![]() CD��
CD��
ͬ����NG��BE��NG=![]() BE��
BE��
��MG=NG��MG��NG��
��2������CD��BE���ཻ��H����ͼ2��
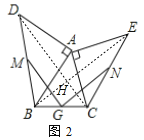
ͬ��1���ķ����ã�MG=NG��MG��NG��
��3������EB��DC���ӳ��ཻ�ڵ�H����ͼ3.
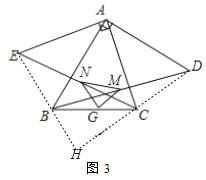
ͬ��1���ķ����ã�MG=NG��
ͬ��1���ķ����ã���ABE�ա�ADC��
���AEB=��ACD��
���CEH+��ECH=��AEH����AEC+180�㩁��ACD����ACE=��ACD��45��+180�㩁��ACD��45��=90�㣬
���DHE=90�㣬
ͬ��1���ķ����ã�MG��NG��
���GMN�ǵ���ֱ��������.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˼�ǿ����Ľ�ˮ��ʶ����������ˮ��Դ��ij���й涨��ˮ�շѱ����£�ÿ��ÿ����ˮ��������6��3ʱ��ˮ�Ѱ�aԪ/��3�շѣ�ÿ��ÿ����ˮ������6��3ʱ���������IJ���ÿ��������aԪ�շѣ������IJ��ְ�cԪ/��3�շѣ�����ij�û�����3��4�·ݵ���ˮ����ˮ�����±���ʾ��
�·� | ��ˮ��(m3) | �շ�(Ԫ) |
3 | 5 | 7.5 |
4 | 9 | 27 |
(1)��a��c��ֵ����д��ÿ����ˮ��������6��3�ͳ���6��3ʱ��ˮ������ˮ��֮��Ĺ�ϵʽ��
(2)��֪ij��5�·ݵ���ˮ��Ϊ8��3������û�5�·ݵ�ˮ�ѣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������Rt��ABC����ACB=90������ֱ�DZ���������DEFG�ı߳���Ϊ2����AC��DE��ͬһֱ���ϣ���ʼʱ��C���D�غϣ�����ABC������ֱ������ƽ�ƣ�ֱ����A���E�غ�Ϊֹ����CD�ij�Ϊx����ABC��������DEFG�غϲ��֣�ͼ����Ӱ���֣������Ϊy����y��x֮��ĺ�����ϵ��ͼ������ǣ�������

A.  B.
B. 
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳���Ӫij��Ʒ�Ƶ���ߣ�����ʱ�ĵ�����30Ԫ�������г����飺��һ��ʱ���ڣ����۵�����40Ԫʱ����������600���������۵���ÿ��1Ԫ���ͻ����۳�10����ߣ�
��1�����������Ʒ����ߵ����۵���ΪxԪ��x��40��������ֱ���x�Ĵ���ʽ����ʾ������y�������۸�Ʒ����������wԪ�����ѽ����д�ڱ����У�
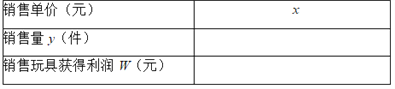
��2���ڣ�1�������£����̳������10000Ԫ�����������������۵���xӦ��Ϊ����Ԫ��
��3���ڣ�1�������£�����߳��涨��Ʒ��������۵��۲�����44Ԫ�����̳�Ҫ��ɲ�����540���������������̳����۸�Ʒ�����õ���������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AD����ABC�Ľ�ƽ���ߣ���E��AB����һ�㣬AE=AC��EF��BC����AC�ڵ�F�����н�����ȷ���ǣ�������
�١�ADE=��ADC������CDE�ǵ��������Σ���CEƽ�֡�DEF����AD��ֱƽ��CE����AD=CE��

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������7����ɫ��ͬ����������ɵij����Σ���֪�м�С�����εı߳�Ϊ1����������ε����Ϊ�� ��

A.45B.48C.63D.64
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ʾ��һ����Ϊ2m����Ϊ2n�ij����Σ���ͼ�������ü������ֳ��ĸ�С�����Σ�Ȼ��ͼ���ķ�ʽƴ��һ�������Σ�
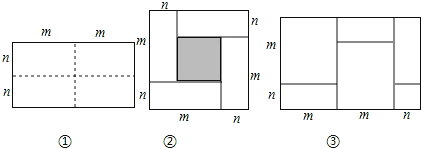
��1����Ҫ����գ�
������Ϊͼ���е���Ӱ���ֵ������εı߳������� ����
���������ֲ�ͬ�ķ�����ʾͼ������Ӱ���ֵ������
����1���� ��
����2���� ��
���۲�ͼ������д������ʽ��m+n��2����m��n��2��mn����������ʽ֮��ĵ�����ϵ���� ����
��2�����ݣ�1�����еĵ�����ϵ������������⣺��|m+n��6|+|mn��4|=0����m��n��2��ֵ��
��3��ʵ����������������ʽ������ͼ�ε��������ʾ����ͼ��������ʾ���� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A��D��C��F��ͬһֱ���ϣ�AB=DE��AD=CF�����������������Բ����ж���ABC�ա�DEF���ǣ�������

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У���֪AB=8��BC=6��������ֱ�����������½ǵĶ���B������ת90��
��ͼ��λ�ã��������½ǵĶ������������ת90����ͼ��λ�á����Դ����ƣ�����������ת2018
�κ���A��������ת��������������·��֮����_________

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com