
【题目】如图,AD是△ABC的角平分线,点E是AB边上一点,AE=AC,EF∥BC,交AC于点F.下列结论正确的是( )
①∠ADE=∠ADC;②△CDE是等腰三角形;③CE平分∠DEF;④AD垂直平分CE;⑤AD=CE.

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
根据三角形全等和等腰三角形的判定、垂直平分线的判定进行依次判定即可.
解:①∵AD是△ABC的角平分线,
∴∠EAD=∠CAD,
在△AED和△ACD中,
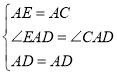 ,
,
∴△AED≌△ACD,
∴∠ADE=∠ADC
故①正确;
②∵△AED≌△ACD,
∴ED=DC,
∴△CDE是等腰三角形;
故②正确;
③∵DE=DC,
∴∠DEC=∠DCE,
∵EF∥BC,
∴∠DCE=∠CEF,
∴∠DEC=∠CEF,
∴CE平分∠DEF,
故③正确;
④∵DE=DC,
∴点D在线段EC的垂直平分线上,
∵AE=AC,
∴点A在线段EC的垂直平分线上,
∴AD垂直平分CE.
故④正确;
⑤∵AD垂直平分CE,
∴当四边形ACDE是矩形时,AD=CE,
故⑤不正确;
故选:B.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】为了解学生体育活动的情况,学校设计了“你最喜欢的体育活动是哪一项(仅限一项)”的调查问卷.该校对学生进行随机抽样调查,以下是根据调查数据得到的不完整的统计图.请根据统计图中信息解答以下问题:
(1)该校对多少名学生进行了抽样调查?
(2)①请补全图1并标上数据,
②图2中x=__________% ;
(3)若该校共有学生900人,请你估计该校最喜欢跳绳项目的学生约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若AC=6,BC=8,OA=2,求线段DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于点A和点B,其中点A的坐标为(﹣2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.
(1)求抛物线的解析式;
(2)若直线BC的函数解析式为y’=kx+b,求当满足y<y’时,自变量x的取值范围.
(3)平行于DE的一条动直线l与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂准备翻建新的大门,厂门要求设计成轴对称的拱形曲线.已知厂门的最大宽度AB=12m,最大高度OC=4m,工厂的运输卡车的高度是3m,宽度是5.8m.现设计了两种方案.方案一:建成抛物线形状(如图1);方案二:建成圆弧形状(如图2).为确保工厂的卡车在通过厂门时更安全,你认为应采用哪种设计方案?请说明理由.
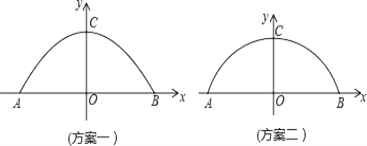
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)操作发现:如图①,小明画了一个等腰三角形ABC,其中AB=AC,在△ABC的外侧分别以AB,AC为腰作了两个等腰直角三角形ABD,ACE,分别取BD,CE,BC的中点M,N,G,连接GM,GN.小明发现了:线段GM与GN的数量关系是__________;位置关系是__________.
(2)类比思考:
如图②,小明在此基础上进行了深入思考.把等腰三角形ABC换为一般的锐角三角形,其中AB>AC,其它条件不变,小明发现的上述结论还成立吗?请说明理由.
(3)深入研究:
如图③,小明在(2)的基础上,又作了进一步的探究.向△ABC的内侧分别作等腰直角三角形ABD,ACE,其它条件不变,试判断△GMN的形状,并给与证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
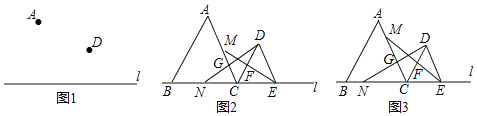
【题目】已知点A、D在直线l的同侧.
(1)如图1,在直线l上找一点C.使得线段AC+DC最小(请通过画图指出点C的位置);
(2)如图2,在直线l上取两点B、E,恰好能使△ABC和△DCE均为等边三角形.M、N分别是线段AC、BC上的动点,连结DN交AC于点G,连结EM交CD于点F.
①当点M、N分别是AC、BC的中点时,判断线段EM与DN的数量关系,并说明理由;
②如图3,若点M、N分别从点A和B开始沿AC和BC以相同的速度向点C匀速运动,当M、N与点C重合时运动停止,判断在运动过程中线段GF与直线1的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.
(1)在方程①3x-1=0;②![]() x+1=0;③x-(3x+1)=-5中,不等式组
x+1=0;③x-(3x+1)=-5中,不等式组![]() 关联方程是______(填序号).
关联方程是______(填序号).
(2)若不等式组 的一个关联方程的根是整数,则这个关联方程可以是______(写出一个即可).
的一个关联方程的根是整数,则这个关联方程可以是______(写出一个即可).
(3)若方程9-x=2x,3+x=2(x+![]() )都是关于x的不等式组
)都是关于x的不等式组![]() 的关联方程,试求出m的取值范围.
的关联方程,试求出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东方专卖店专销某种品牌的钢笔,进价12元/支,售价20元/支.为了促销,专卖店决定凡是买10支以上的,每多买一支,售价就降低0.10元(例如,某人买20支钢笔,于是每只降价0.10×(20﹣10)=1元,就可以按19元/支的价格购买),但是最低价为16元/支.
(1)求顾客一次至少买多少支,才能以最低价购买?
(2)写出当一次购买x支时(x>10),利润y(元)与购买量x(支)之间的函数关系式;
(3)有一天,一位顾客买了46支,另一位顾客买了50支,专实店发现卖了50支反而比卖46支赚的钱少,为了使每次卖的多赚钱也多,在其他促销条件不变的情况下,最低价16元/支至少要提高到多少,为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com