
����Ŀ����֪��A��D��ֱ��l��ͬ�࣮
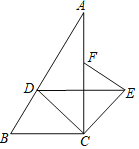
��1����ͼ1����ֱ��l����һ��C��ʹ���߶�AC+DC��С����ͨ����ͼָ����C��λ�ã���
��2����ͼ2����ֱ��l��ȡ����B��E��ǡ����ʹ��ABC����DCE��Ϊ�ȱ������Σ�M��N�ֱ����߶�AC��BC�ϵĶ��㣬����DN��AC�ڵ�G������EM��CD�ڵ�F��
�ٵ���M��N�ֱ���AC��BC���е�ʱ���ж��߶�EM��DN��������ϵ����˵�����ɣ�
����ͼ3������M��N�ֱ�ӵ�A��B��ʼ��AC��BC����ͬ���ٶ����C�����˶�����M��N���C�غ�ʱ�˶�ֹͣ���ж����˶��������߶�GF��ֱ��1��λ�ù�ϵ����˵�����ɣ�
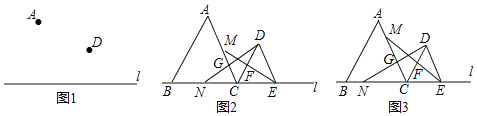
���𰸡���1����������2����EM=DN��FG��l
��������
��1����������A����ֱ��l�ĶԳƵ�A'����DA'��ֱ��l�ڵ�C��
��2�������жϳ�CM=CN����DCN=��ECM=120���������жϳ���CDN�ա�CEM�����ɵó����ۣ�
��ͬ�ٵķ����жϳ���CDN�ա�CEM���ó���CDN=��CEM�������жϳ���DCG�ա�ECF���ó�CF=CG���ó���CFG�ǵȱ������μ��ɵó����ۣ�
��1����ͼ1��ʾ����C������������

��2����EM=DN�����ɣ�
�ߵ�M��N�ֱ���AC��BC���е㣬
��CM=![]() AC��CN=
AC��CN=![]() BC��
BC��
�ߡ�ABC�ǵȱ������Σ�
���ACB=60����AC=BC��
���ECM=120����CM=CN��
���CDE�ǵȱ������Σ�
���DCE=60����CE=CD�����NCD=120����
����CDN����CEM��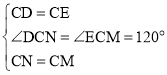 ��
��
���CDN�ա�CEM��
��EM=DN��
��FG��l�����ɣ���ͼ3������FG��

���˶�֪��AM=BN��
��AC=BC��
��CM=BN��
����CDN����CEM��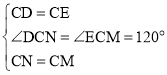 ��
��
���CDN�ա�CEM��
���CDN=��CEM��
�ߡ�ACB=��DCE=60����
���ACD=60��=��DCE��
����DCG����ECF�� ��
��
���DCG�ա�ECF��
��CF=CG��
�ߡ�FCG=60����
���CFG�ǵȱ������Σ�
���CFG=60��=��ECF��
��FG��BC��
����FG��l��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��һ�κ���y=kx+b��ͼ���뷴��������y=��![]() ��ͼ����A��B���㣬�ҵ�A�ĺ�����͵�B�������궼�ǩ�2��
��ͼ����A��B���㣬�ҵ�A�ĺ�����͵�B�������궼�ǩ�2��
��1����һ�κ����Ľ���ʽ��
��2�����AOB�������
��3��ֱ��д��kx+b+![]() ��0�Ľ⼯��
��0�Ľ⼯��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧ���Ԫһ�η������Ӧ��֮����ʦд����һ�����������£�![]() ��Ҫ�����������鸳��ʵ���龳��
��Ҫ�����������鸳��ʵ���龳��
С��˵����һ���龳��ѧУ����������С�飬�鷨��������飬�����鷨��������Ķ������������5�ˣ��鷨��ƽ��ÿ�������4���鷨��Ʒ��������ƽ��ÿ�������3��������Ʒ������С�鹲�����40����Ʒ�����鷨�����������ж����ˣ�
С��ͨ����֤����С��������龳�����⣬���ҳ��������ģ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AD����ABC�Ľ�ƽ���ߣ���E��AB����һ�㣬AE=AC��EF��BC����AC�ڵ�F�����н�����ȷ���ǣ�������
�١�ADE=��ADC������CDE�ǵ��������Σ���CEƽ�֡�DEF����AD��ֱƽ��CE����AD=CE��

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�E�DZ�AB�ϵ�һ���㣨�����A��B�غϣ�������DE����A����ֱ��DE�ĶԳƵ�ΪF������EF���ӳ���BC�ڵ�G������DG������E��EH��DE��DG���ӳ����ڵ�H������BH��
��1����֤��GF=GC��
��2���õ�ʽ��ʾ�߶�BH��AE��������ϵ����֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ʾ��һ����Ϊ2m����Ϊ2n�ij����Σ���ͼ�������ü������ֳ��ĸ�С�����Σ�Ȼ��ͼ���ķ�ʽƴ��һ�������Σ�
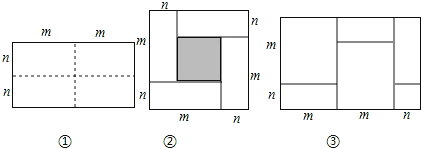
��1����Ҫ����գ�
������Ϊͼ���е���Ӱ���ֵ������εı߳������� ����
���������ֲ�ͬ�ķ�����ʾͼ������Ӱ���ֵ������
����1���� ��
����2���� ��
���۲�ͼ������д������ʽ��m+n��2����m��n��2��mn����������ʽ֮��ĵ�����ϵ���� ����
��2�����ݣ�1�����еĵ�����ϵ������������⣺��|m+n��6|+|mn��4|=0����m��n��2��ֵ��
��3��ʵ����������������ʽ������ͼ�ε��������ʾ����ͼ��������ʾ���� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����̶�ֱ����ͼ��������⣺
��ͼ��![]() ��
��![]() ���ǵȱ������Σ���
���ǵȱ������Σ���![]() �ڲ���һ��
�ڲ���һ��![]() ��ʹ��
��ʹ��![]() ��������֤����
��������֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ֱ��������![]() �Ķ���
�Ķ���![]() ��
��![]() ���ϣ�
���ϣ�![]() ����
����![]() ��
��![]() ��
��![]() ����
����![]() ��
��

��1�����![]() �����ꣻ
�����ꣻ
��2������![]() ����
����![]() �������
�������
��3����![]() ������һ����
������һ����![]() ����
����![]() ��ֵ��Сʱ�����ʱ
��ֵ��Сʱ�����ʱ![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACB=90�㣬CDƽ�֡�ACB��AB�ڵ�D������CDB�Ƶ�C˳ʱ����ת����CEF��λ�ã���F��AC�ϣ�
��1����CDB��ת�Ķ�������2������DE���ж�DE��BC��λ�ù�ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com