
【题目】如图,在△ABC中,∠ACB=90°,CD平分∠ACB交AB于点D,将△CDB绕点C顺时针旋转到△CEF的位置,点F在AC上.
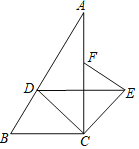
(1)△CDB旋转的度数;(2)连结DE,判断DE与BC的位置关系,并说明理由.
【答案】(1)△CDB旋转的度数:90°;(2)DE∥BC,见解析.
【解析】
(1)根据旋转的性质确定旋转角的度数;
(2)先利用旋转的性质得∠DCE=∠BCF=90°,CD=CE,则可判断△CDE为等腰直角三角形,所以∠CDE=45°,再利用角平分线定义得到∠BCD=45°,则∠CDE=∠BCD,然后根据平行线的判定方法可判断DE∥BC.
解:(1)∵将△CDB绕点C顺时针旋转到△CEF的位置,点F在AC上,
∴旋转角为∠BCF,
即旋转角为90°;
(2)DE∥BC.
理由如下:∵将△CDB绕点C顺时针旋转到△CEF的位置,点F在AC上,
∴∠DCE=∠BCF=90°,CD=CE,
∴△CDE为等腰直角三角形,
∴∠CDE=45°,
∵CD平分∠ACB交AB于点D,
∴∠BCD=45°,
∴∠CDE=∠BCD,
∴DE∥BC.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:
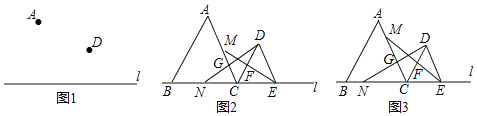
【题目】已知点A、D在直线l的同侧.
(1)如图1,在直线l上找一点C.使得线段AC+DC最小(请通过画图指出点C的位置);
(2)如图2,在直线l上取两点B、E,恰好能使△ABC和△DCE均为等边三角形.M、N分别是线段AC、BC上的动点,连结DN交AC于点G,连结EM交CD于点F.
①当点M、N分别是AC、BC的中点时,判断线段EM与DN的数量关系,并说明理由;
②如图3,若点M、N分别从点A和B开始沿AC和BC以相同的速度向点C匀速运动,当M、N与点C重合时运动停止,判断在运动过程中线段GF与直线1的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班数学课外活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处测得树顶端D的仰角为60°,已知A点的高度AB为2米,台阶AC的坡度i=1:2,且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测倾器的高度忽略不计,结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东方专卖店专销某种品牌的钢笔,进价12元/支,售价20元/支.为了促销,专卖店决定凡是买10支以上的,每多买一支,售价就降低0.10元(例如,某人买20支钢笔,于是每只降价0.10×(20﹣10)=1元,就可以按19元/支的价格购买),但是最低价为16元/支.
(1)求顾客一次至少买多少支,才能以最低价购买?
(2)写出当一次购买x支时(x>10),利润y(元)与购买量x(支)之间的函数关系式;
(3)有一天,一位顾客买了46支,另一位顾客买了50支,专实店发现卖了50支反而比卖46支赚的钱少,为了使每次卖的多赚钱也多,在其他促销条件不变的情况下,最低价16元/支至少要提高到多少,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
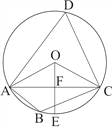
【题目】如图,四边形ABCD 是⊙O的内接四边形,∠ABC=2∠D,连接OA,OC,AC
(1)求∠OCA的度数 (2)如果OE![]() AC于F,且OC=
AC于F,且OC=![]() , 求AC的长
, 求AC的长
查看答案和解析>>
科目:初中数学 来源: 题型:
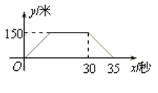
【题目】为了预防“甲型H1N1”,某校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题:
(1)药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?
(2)研究表明,当空气中每立方米的含药量低于1.6mg时,生方可进教室,那么从消毒开始,至少需要几分钟后,生才能进入教室?
(3)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】火车匀速通过隧道时,火车在隧道内的长度![]() (米)与火车行驶时间
(米)与火车行驶时间![]() (秒)之间的关系用图象描述如图所示,有下列结论:
(秒)之间的关系用图象描述如图所示,有下列结论:
①火车的长度为120米;
②火车的速度为30米/秒;
③火车整体都在隧道内的时间为25秒;
④隧道长度为750米.
其中正确的结论是_____.(把你认为正确结论的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com