
【题目】已知如图,等腰梯形ABCD,AB=CD,BE=CE,求证:AE=DE.

【答案】见解析
【解析】【试题分析】
等腰梯形ABCD,AB=CD,根据等腰梯形的性质得:∠ABC=∠DCB,因为BE=CE,根据等边对等角得:∠EBC=∠ECB;根据等式的性质得:∠EBC﹣∠ABC=∠ECB﹣∠DCB,即∠EBA=∠ECD;在△EBA和△ECD中,AB=CD,∠EBA=∠ECD,BE=CE,根据边角边定理得:△EBA≌△ECD(SAS),根据全等三角形的性质得:AE=DE.
【试题解析】
∵等腰梯形ABCD,AB=CD,
∴∠ABC=∠DCB,
∵BE=CE,
∴∠EBC=∠ECB,
∴∠EBC﹣∠ABC=∠ECB﹣∠DCB,
即∠EBA=∠ECD,
在△EBA和△ECD中,
AB=CD,∠EBA=∠ECD,BE=CE,
∴△EBA≌△ECD(SAS),
∴AE=DE.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】小红和小明在操场做游戏,他们先在地上画了半径分别2m和3m的同心圆(如图),蒙上眼在一定距离外向圈内掷小石子,掷中阴影小红胜,否则小明胜,未掷入圈内不算,你来当裁判.
(1)你认为游戏公平吗?为什么?
(2)游戏结束,小明边走边想,“反过来,能否用频率估计概率的方法,来估算某一不规则图形的面积呢”.请你设计方案,解决这一问题.(要求补充完整图形,说明设计步骤、原理,写出估算公式)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,CD平分∠ACB交AB于点D,将△CDB绕点C顺时针旋转到△CEF的位置,点F在AC上.
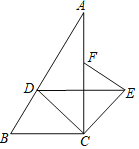
(1)△CDB旋转的度数;(2)连结DE,判断DE与BC的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,F、G是AD边上的两个点,且FC平分∠BCD,GB平分∠ABC,FC与GB交于点E.
①AB=AG;②连接BF、CG,则四边形BFGC为等腰梯形;③AF=DG;④△ABG∽△DCF.
以上四个结论中一定成立的有( )个.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A=70°,若三角形内有一点P到三边的距离相等,则∠BPC=_____;若三角形内有一点M到三个顶点的距离相等,则∠BMC=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市政公司为绿化建设路风景带,计划购买甲乙两种树苗600株,甲种树苗每株50元,乙种树苗每株70元.有关统计表明,甲乙两种树苗的成活率分别为80%和95%.(注:成活率=![]() ×100%).
×100%).
(1)若购买树苗的钱不超过40000元,应如何选购甲、乙两种树苗;
(2)若希望这批树苗的成活率不低于90%,且购买树苗的费用最低,应如何选购甲、乙两种树苗并求出最低费用是多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC在平面直角坐标系中的位置如图所示.
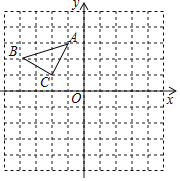
(1)画出把△ABC先向下平移3个单位,再向右平移4个单位后所得到的△A1B1C1;
(2)写出A1,B1,C1的坐标;
(3)求△A1B1C1的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com