
【题目】东方专卖店专销某种品牌的钢笔,进价12元/支,售价20元/支.为了促销,专卖店决定凡是买10支以上的,每多买一支,售价就降低0.10元(例如,某人买20支钢笔,于是每只降价0.10×(20﹣10)=1元,就可以按19元/支的价格购买),但是最低价为16元/支.
(1)求顾客一次至少买多少支,才能以最低价购买?
(2)写出当一次购买x支时(x>10),利润y(元)与购买量x(支)之间的函数关系式;
(3)有一天,一位顾客买了46支,另一位顾客买了50支,专实店发现卖了50支反而比卖46支赚的钱少,为了使每次卖的多赚钱也多,在其他促销条件不变的情况下,最低价16元/支至少要提高到多少,为什么?
【答案】(1)50支;(2)当10<x≤50时,y=﹣0.1x2+9x, 当x>50时,y =4x;(3)16.5元.
【解析】试题分析:(1)已知每多买一支,售价就降低0.1元,那就是多买了![]() 支,故一次至少买
支,故一次至少买![]() +10=50支;
+10=50支;
(2)当10<x≤50时,每支钢笔的利润为20﹣0.1(x﹣10)﹣12,故y与x之间的函数关系式为y=[20﹣0.1(x﹣10)﹣12]x=﹣0.1x2+9x;当x>50时,y=(16﹣12)x=4x;
(3)根据题意列出表格,由表格可得知.
试题解析:(1)由题意得:
![]() +10=50支;
+10=50支;
(2)当10<x≤50时(1分),
y=[20﹣0.1(x﹣10)﹣12]x=﹣0.1x2+9x,
当x>50时(1分),y=(16﹣12)x=4x;
(3)方法(一):列表
x | … | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | … |
y | … | 200 | 200.9 | 201.6 | 202.1 | 202.4 | 202.5 | 202.4 | 202.1 | 201.6 | 200.9 | 200 |
由表格可知,最低售价为20﹣0.1(45﹣10)=16.5元;
方法(二):利润y=﹣0.1x2+9x=﹣0.1(x﹣45)2+202.5,
∵卖的越多赚的越多,即y随x的增大而增大,
∴由二次函数图象可知,x≤45,最低售价为20﹣0.1(45﹣10)=16.5元.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,点E是AB边上一点,AE=AC,EF∥BC,交AC于点F.下列结论正确的是( )
①∠ADE=∠ADC;②△CDE是等腰三角形;③CE平分∠DEF;④AD垂直平分CE;⑤AD=CE.

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,等腰直角三角形![]() 的顶点
的顶点![]() 在
在![]() 轴上,
轴上,![]() ,且
,且![]() ,
,![]() 交
交![]() 轴于
轴于![]() ,
,

(1)求点![]() 的坐标;
的坐标;
(2)连接![]() ,求
,求![]() 的面积;
的面积;
(3)在![]() 轴上有一动点
轴上有一动点![]() ,当
,当![]() 的值最小时,求此时
的值最小时,求此时![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
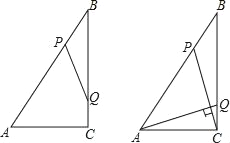
(1)若△BPQ与△ABC相似,求t的值;
(2)连接AQ、CP,若AQ⊥CP,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红和小明在操场做游戏,他们先在地上画了半径分别2m和3m的同心圆(如图),蒙上眼在一定距离外向圈内掷小石子,掷中阴影小红胜,否则小明胜,未掷入圈内不算,你来当裁判.
(1)你认为游戏公平吗?为什么?
(2)游戏结束,小明边走边想,“反过来,能否用频率估计概率的方法,来估算某一不规则图形的面积呢”.请你设计方案,解决这一问题.(要求补充完整图形,说明设计步骤、原理,写出估算公式)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,已知AB=8,BC=6,矩形在直线上绕其右下角的顶点B向右旋转90°
至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置……以此类推,这样连续旋转2018
次后,顶点A在整个旋转过程中所经过的路线之和是_________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,CD平分∠ACB交AB于点D,将△CDB绕点C顺时针旋转到△CEF的位置,点F在AC上.
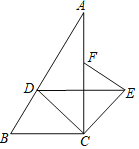
(1)△CDB旋转的度数;(2)连结DE,判断DE与BC的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A=70°,若三角形内有一点P到三边的距离相等,则∠BPC=_____;若三角形内有一点M到三个顶点的距离相等,则∠BMC=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车制造厂开发一款新式电动汽车,计划一年生产安装![]() 辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人.他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:
辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人.他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:![]() 名熟练工和
名熟练工和![]() 名新工人每月可安装
名新工人每月可安装![]() 辆电动汽车;
辆电动汽车;![]() 名熟练工和
名熟练工和![]() 名新工人每月可安装
名新工人每月可安装![]() 辆电动汽车.
辆电动汽车.
(1)每名熟练工和新工人每月分别可以安装多少辆电动汽车?
(2)如果工厂招聘![]() 名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?
名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com