
����Ŀ��ѧ���Ԫһ�η������Ӧ��֮����ʦд����һ�����������£�![]() ��Ҫ�����������鸳��ʵ���龳��
��Ҫ�����������鸳��ʵ���龳��
С��˵����һ���龳��ѧУ����������С�飬�鷨��������飬�����鷨��������Ķ������������5�ˣ��鷨��ƽ��ÿ�������4���鷨��Ʒ��������ƽ��ÿ�������3��������Ʒ������С�鹲�����40����Ʒ�����鷨�����������ж����ˣ�
С��ͨ����֤����С��������龳�����⣬���ҳ��������ģ�
���𰸡�С������������Ϊδ֪�������龳���裮
��������
����С����Ƶ��龳�����鷨����x�ˣ���������y�ˣ������鷨��������Ķ������������5�ˣ��鷨��ƽ��ÿ�������4���鷨��Ʒ��������ƽ��ÿ�������3��������Ʒ������С�鹲�����40����Ʒ���г������飬�ɵó�x��y��ֵ��������ֻ���ǷǸ���������x=5.5�����ɵó�С��������龳�����⣮
���鷨����x�ˣ���������y�ˣ�
��������ã�![]() ��
��
��ã�![]() ��
��
������ֻ���ǷǸ���������x��5.5��
��С������������Ϊδ֪�������龳���裮


 ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��B�������30ǧ�ף�ij������12��30�ּ������г���A�س���ʻ��B�أ���Ҳ��ͬ��������Ħ�г���A�س���ʻ��B�أ�ͼ������PQR���߶�MN�ֱ��ʾ��������ʻ��·��S(ǧ��)���������ʱ��t��ʱ���Ĺ�ϵ���Ը���ͼ�е���Ϣ����������⣺

��1���׳�����Сʱ���Ҳų�����
��2������ʻ����Сʱ���ϼף���ʱ���˾���B�ػ��ж���ǧ�ף�
��3���״�����12��30��14��30��ƽ���ٶ��Ƕ���ǧ�ף�ʱ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��AB//ED, BFƽ�֡�ABC, DFƽ�֡�EDC.
(1)����ABC =130������EDC=110��,���C�Ķ����͡�BFD�Ķ���;
(2)��ֱ��д����BFD���C�Ĺ�ϵ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���C=90������O��AC�ϣ���OAΪ�뾶����O��AB�ڵ�D��BD�Ĵ�ֱƽ���߽�BC�ڵ�E����BD�ڵ�F������DE��
��1���ж�ֱ��DE����O��λ�ù�ϵ����˵�����ɣ�
��2����AC=6��BC=8��OA=2�����߶�DE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��P�ǵȱ�������ABC�ڵ�һ�㣬����PA��PB��PC����BPΪ������PBQ=60������BQ=BP������CQ��
(1) �۲첢����AP��CQ֮��Ĵ�С��ϵ����֤����Ľ��ۣ�
(2) ��PA��PB��PC=3��4��5������PQ�����ж���PQC����״����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c��a��0����y�ύ�ڵ�C��0��4������x�ύ�ڵ�A�͵�B�����е�A������Ϊ����2��0���������ߵĶԳ���x=1�������߽��ڵ�D����ֱ��BC���ڵ�E��
��1���������ߵĽ���ʽ��
��2����ֱ��BC�ĺ�������ʽΪy��=kx+b,������y<y��ʱ���Ա���x��ȡֵ��Χ.
��3��ƽ����DE��һ����ֱ��l��ֱ��BC�ཻ�ڵ�P�����������ཻ�ڵ�Q������D��E��P��QΪ������ı�����ƽ���ı��Σ����P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����������µĴ��ţ�����Ҫ����Ƴ���ԳƵĹ�������.��֪���ŵ�������AB=12m�����߶�OC=4m�����������俨���ĸ߶���3m��������5.8m.����������ַ���.����һ��������������״����ͼ1����������������Բ����״����ͼ2��.Ϊȷ�������Ŀ�����ͨ������ʱ����ȫ������ΪӦ����������Ʒ�������˵������.
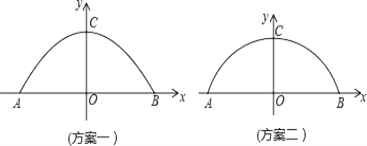
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��D��ֱ��l��ͬ�࣮
��1����ͼ1����ֱ��l����һ��C��ʹ���߶�AC+DC��С����ͨ����ͼָ����C��λ�ã���
��2����ͼ2����ֱ��l��ȡ����B��E��ǡ����ʹ��ABC����DCE��Ϊ�ȱ������Σ�M��N�ֱ����߶�AC��BC�ϵĶ��㣬����DN��AC�ڵ�G������EM��CD�ڵ�F��
�ٵ���M��N�ֱ���AC��BC���е�ʱ���ж��߶�EM��DN��������ϵ����˵�����ɣ�
����ͼ3������M��N�ֱ�ӵ�A��B��ʼ��AC��BC����ͬ���ٶ����C�����˶�����M��N���C�غ�ʱ�˶�ֹͣ���ж����˶��������߶�GF��ֱ��1��λ�ù�ϵ����˵�����ɣ�
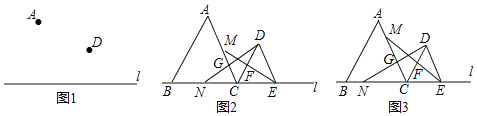
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ѧ����С���ͬѧ����������һ����DE�ĸ߶ȣ��������������ǰ��һ¥ͤǰ��̨����A�㴦���������D������Ϊ30��������������ķ����ߵ�̨���µĵ�C�����������D������Ϊ60������֪A��ĸ߶�ABΪ2�ף�̨��AC���¶�i=1��2����B��C��E������ͬһ��ֱ���ϣ�������������������DE�ĸ߶ȣ����������ĸ߶Ⱥ��Բ��ƣ�����������ţ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com