
【题目】如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
(1) 观察并猜想AP与CQ之间的大小关系,并证明你的结论;
(2) 若PA:PB:PC=3:4:5,连接PQ,试判断△PQC的形状,并说明理由.

【答案】(1)AP=CQ,证明见解析(2)△PQC是直角三角形,证明见解析
【解析】
根据等边三角形的性质利用SAS判定△ABP≌△CBQ,从而得到AP=CQ;设PA=3a,PB=4a,PC=5a,由已知可判定△PBQ为正三角形从而可得到PQ=4a,再根据勾股定理判定△PQC是直角三角形.
(1)猜想:AP=CQ,
证明:∵∠ABP+∠PBC=60°,∠QBC+∠PBC=60°,
∴∠ABP=∠QBC.
又AB=BC,BP=BQ,
∴△ABP≌△CBQ,
∴AP=CQ;
(2)由PA:PB:PC=3:4:5,

可设PA=3a,PB=4a,PC=5a,
连接PQ,在△PBQ中
由于PB=BQ=4a,且∠PBQ=60°,
∴△PBQ为正三角形.
∴PQ=4a.
于是在△PQC中
∵PQ![]() +QC
+QC![]() =16a
=16a![]() +9a
+9a![]() =25a
=25a![]() =PC
=PC![]()
∴△PQC是直角三角形.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
【题目】材料阅读:材料1:符号“ ”称为二阶行列式,规定它的运算法则为
”称为二阶行列式,规定它的运算法则为 .如
.如![]() .
.
材料2:我们已经学习过求解一元一次方程、二元一次方程组、分式方程等方程的解法,虽然各类方程的解法不尽相同,但是蕴含了相同的基本数学思想——转化,把未知转化为已知.用“转化”的数学思想,还可以解一些新的方程.例如,求解部分一元二次方程![]() 时,我们可以利用因式分解把它转化为一元一次方程来求解.如解方程:
时,我们可以利用因式分解把它转化为一元一次方程来求解.如解方程:![]() .∵
.∵![]() ∴
∴![]() .故
.故![]() 或
或![]() .因此原方程的解是
.因此原方程的解是![]() ,
,![]() .
.
根据材料回答以下问题:
(1)二阶行列式![]() ___________;二阶行列式
___________;二阶行列式![]() 中
中![]() 的值为__________.
的值为__________.
(2)求解![]() 中
中![]() 的值.
的值.
(3)结合材料,若![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
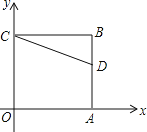
【题目】如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
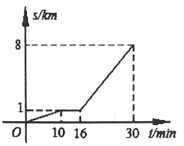
【题目】小亮从家步行到公交站台,等公交车去学校.图中折线表示小亮的行程![]() 与所花时间
与所花时间![]() 之间的函数关系.下列说法:
之间的函数关系.下列说法:![]() 他离家
他离家![]() 共用了
共用了![]() ;
;![]() 他等公交车的时间是
他等公交车的时间是![]() ;
;![]() 他步行的速度是
他步行的速度是![]() ;
;![]() 公交车的速度是
公交车的速度是![]() .正确的有________________(只填正确说法的序号).
.正确的有________________(只填正确说法的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学完二元一次方程组的应用之后,老师写出了一个方程组如下:![]() ,要求把这个方程组赋予实际情境.
,要求把这个方程组赋予实际情境.
小军说出了一个情境:学校有两个课外小组,书法组和美术组,其中书法组的人数的二倍比美术组多5人,书法组平均每人完成了4幅书法作品,美术组平均每人完成了3幅美术作品,两个小组共完成了40幅作品,问书法组和美术组各有多少人?
小明通过验证后发现小军赋予的情境有问题,请找出问题在哪?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是边AB上的一动点(不与点A、B重合),连接DE,点A关于直线DE的对称点为F,连接EF并延长交BC于点G,连接DG,过点E作EH⊥DE交DG的延长线于点H,连接BH.
(1)求证:GF=GC;
(2)用等式表示线段BH与AE的数量关系,并证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com