
【题目】如图所示,一次函数y=kx+b的图象与反比例函数y=﹣![]() 的图象交于A、B两点,且点A的横坐标和点B的纵坐标都是﹣2,
的图象交于A、B两点,且点A的横坐标和点B的纵坐标都是﹣2,
(1)求一次函数的解析式;
(2)求△AOB的面积.
(3)直接写出kx+b+![]() >0的解集.
>0的解集.

【答案】(1)y=﹣x+2;(2)6;(3)由函数图象可得当x<﹣2或0<x<4时,kx+b+![]() >0.
>0.
【解析】试题分析:(1)先求出A,B两点坐标,将其代入一次函数关系式即可;
(2)根据一次函数与y轴的交点为(0,2),则△AOC和△BOC的底边长为2,两三角形的高分别为|x1|和|x2|,从而可求得其面积;
(3)由函数图象得出直线在双曲线上方时x的取值范围.
试题解析:(1)设A(x1,y1),B(x2,y2),则x1=﹣2,y2=﹣2,
把x1=y2=﹣2分别代入y=﹣![]() 得y1=x2=4,
得y1=x2=4,
∴A(﹣2,4),B(4,﹣2).
把A(﹣2,4)和B(4,﹣2)分别代入y=kx+b,
得![]() ,
,
解得![]() ,
,
∴一次函数的解析式为y=﹣x+2;
(2)如图,
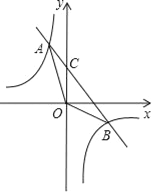
∵y=﹣x+2与y轴交点为C(0,2),
∴OC=2,
∴S△AOB=S△AOC+S△BOC=![]() ×OC×|x1|+
×OC×|x1|+![]() ×OC×|x2|=
×OC×|x2|=![]() ×2×2+
×2×2+![]() ×2×4=6;
×2×4=6;
(3)由函数图象可得当x<﹣2或0<x<4时,kx+b+![]() >0.
>0.


科目:初中数学 来源: 题型:
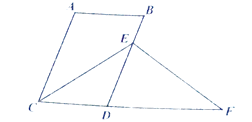
【题目】如图,AB∥CD, AC∥BD, CE平分∠ACD,交BD于点E,点F在CD的延长线上,且∠BEF=∠CEF,若∠DEF=∠EDF,则∠A的度数为_____![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地相距30千米,某日下午12点30分甲骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车从A地出发驶往B地,图中折线PQR和线段MN分别表示甲和乙所行驶的路程S(千米)与该日下午时间t(时)的关系,试根据图中的信息解答以下问题:

(1)甲出发几小时后,乙才出发?
(2)乙行驶多少小时后追上甲,这时两人距离B地还有多少千米?
(3)甲从下午12:30到14;30的平均速度是多少千米/时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生体育活动的情况,学校设计了“你最喜欢的体育活动是哪一项(仅限一项)”的调查问卷.该校对学生进行随机抽样调查,以下是根据调查数据得到的不完整的统计图.请根据统计图中信息解答以下问题:
(1)该校对多少名学生进行了抽样调查?
(2)①请补全图1并标上数据,
②图2中x=__________% ;
(3)若该校共有学生900人,请你估计该校最喜欢跳绳项目的学生约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家买了一辆小轿车,小明连续记录了某一周每天行驶的路程:
星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 | |
路程(千米) |
|
|
|
|
|
|
|
请你用学过的知识解决下面的问题:
(1)请你估计小明家的轿车每月(按![]() 天计算)要行驶多少千米?
天计算)要行驶多少千米?
(2)已知每行驶![]() 千米需汽油
千米需汽油![]() 升,汽油每升
升,汽油每升![]() 元,试用含
元,试用含![]() 、
、![]() 的代数式表示小明家每月的汽油费,此代数式为_______;
的代数式表示小明家每月的汽油费,此代数式为_______;
(3)设![]() ,
,![]() ,请你求出小明家一年(按
,请你求出小明家一年(按![]() 个月计算)的汽油费用大约是多少元(精确到千元).(注:第(1)、(3)小题须写出必要步骤)
个月计算)的汽油费用大约是多少元(精确到千元).(注:第(1)、(3)小题须写出必要步骤)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A点坐标为(﹣4,﹣3),将线段OA绕原点O顺时针旋转90°得到OA′,则点A′的坐标是( )

A. (﹣4,3) B. (﹣3,4) C. (3,﹣4) D. (4,﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,AB//ED, BF平分∠ABC, DF平分∠EDC.
(1)若∠ABC =130°,∠EDC=110°,求∠C的度数和∠BFD的度数;
(2)请直接写出∠BFD与∠C的关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若AC=6,BC=8,OA=2,求线段DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
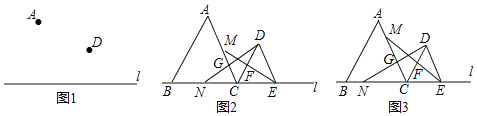
【题目】已知点A、D在直线l的同侧.
(1)如图1,在直线l上找一点C.使得线段AC+DC最小(请通过画图指出点C的位置);
(2)如图2,在直线l上取两点B、E,恰好能使△ABC和△DCE均为等边三角形.M、N分别是线段AC、BC上的动点,连结DN交AC于点G,连结EM交CD于点F.
①当点M、N分别是AC、BC的中点时,判断线段EM与DN的数量关系,并说明理由;
②如图3,若点M、N分别从点A和B开始沿AC和BC以相同的速度向点C匀速运动,当M、N与点C重合时运动停止,判断在运动过程中线段GF与直线1的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com