
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上一点,连接
边上一点,连接![]() ,
,![]() .
. ![]() 与
与![]() 交于点
交于点![]() ,且
,且![]() ∥
∥![]() .
.
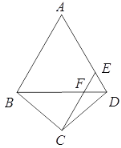
(1)求证:![]() ;
;
(2)若![]() ,
,![]() . 求
. 求![]() 的长 .
的长 .
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)由等边三角形的判定定理可得△ABD为等边三角形,又由平行进行角度间的转化可得出结论.
(2)连接AC交BD于点O,由题意可证AC垂直平分BD,△ABD是等边三角形,可得∠BAO=∠DAO=30°,AB=AD=BD=8,BO=OD=4,通过证明△EDF是等边三角形,可得DE=EF=DF=2,由勾股定理可求OC,BC的长.
(1)证明:∵![]() ,
,![]() ,
,
∴△![]() 是等边三角形.
是等边三角形.
∴![]() .
.
∵![]() ∥
∥![]() ,
,
∴![]() .
.
∴![]() .
.
(2)解:连接![]() 交
交![]() 于点
于点![]() ,
,

∵![]() ,
,![]() ,
,
∴![]() 垂直平分
垂直平分![]() .
.
∴![]() .
.
∵△![]() 是等边三角形,
是等边三角形,![]()
∴![]() ,
,
∴![]() .
.
∵![]() ∥
∥![]() ,
,
∴![]() .
.
∴![]() ,
, ![]() .
.
∵![]() .
.
∴![]() .
.
∴△![]() 是等边三角形.
是等边三角形.
∴![]() ,
,
∴![]() ,
,![]() .
.
在Rt△![]() 中,
中,
∴![]() .
.
在Rt△![]() 中,
中,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,为一圆洞门.工匠在建造过程中需要一根横梁AB和两根对称的立柱CE、DF来支撑,点A、B、C、D在⊙O上,CE⊥AB于E,DF⊥AB于F,且AB=2![]() ,EF=
,EF=![]() ,
,![]() =120°.
=120°.
(1)求出圆洞门⊙O的半径;
(2)求立柱CE的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() 的图象经过点
的图象经过点![]() 则
则
(1)求这个函数表达式;
(2)画出该函数的图像;
(3)写出把这条直线向下平移![]() 个单位长度后的函数关系式是
个单位长度后的函数关系式是
(4)求平移后的图像与两条坐标轴围成的三角形的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系中,直线![]() 交坐标轴于A、B两点,过点C(
交坐标轴于A、B两点,过点C(![]() ,0)作CD交AB于D,交
,0)作CD交AB于D,交![]() 轴于点E.且△COE≌△BOA.
轴于点E.且△COE≌△BOA.

(1)求B点坐标为 ;线段OA的长为 ;
(2)确定直线CD解析式,求出点D坐标;
(3)如图2,点M是线段CE上一动点(不与点C、E重合),ON⊥OM交AB于点N,连接MN.
①点M移动过程中,线段OM与ON数量关系是否不变,并证明;
②当△OMN面积最小时,求点M的坐标和△OMN面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有![]() ,
,![]() 两个不透明的袋子,分别装有3个除颜色外完全相同的小球,其中
两个不透明的袋子,分别装有3个除颜色外完全相同的小球,其中![]() 袋中装有2个白球,1个红球;
袋中装有2个白球,1个红球;![]() 袋中装有2个红球,1个白球.小林和小华商定了一个游戏规则:从摇匀后的
袋中装有2个红球,1个白球.小林和小华商定了一个游戏规则:从摇匀后的![]() ,
,![]() 两袋中各随机摸出一个小球,摸出的这两个小球,若颜色相同,则小林获胜;若颜色不同,则小华获胜.请用列表法或画树状图法,说明这个游戏对双方是否公平.
两袋中各随机摸出一个小球,摸出的这两个小球,若颜色相同,则小林获胜;若颜色不同,则小华获胜.请用列表法或画树状图法,说明这个游戏对双方是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
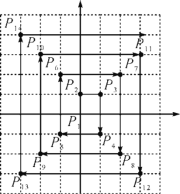
【题目】如图,在平面直角坐标系中,每个最小方格的边长均为1个单位长度,P1,P2,P3,…均在格点上,其顺序按图中“→”方向排列,如:P1(0,0),P2(0,1),P3(1,1),P4(1,-1),P5(-1,-1),P6(-1,2),…,根据这个规律,点P2 019的坐标为_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,五边形ABCDE中有一正三角形ACD,若AB=DE,BC=AE,∠E=115°,则∠BAE的度数为何?( )

A. 115 B. 120 C. 125 D. 130
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任意抛掷一枚均匀的骰子,朝上面的点数为![]() 的概率为
的概率为![]() ,下列说法正确吗?为什么?
,下列说法正确吗?为什么?
![]() 任意抛掷一枚均匀的骰子
任意抛掷一枚均匀的骰子![]() 次,朝上面的点数为
次,朝上面的点数为![]() 的次数为
的次数为![]() 次.
次.
![]() 任意抛掷一枚均匀的骰子
任意抛掷一枚均匀的骰子![]() 次,朝上面的点数为
次,朝上面的点数为![]() 的次数大约为
的次数大约为![]() 次.
次.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB=AC,CO的延长线交AB于点D.
(1)求证:AO平分∠BAC;
(2)若BC=6,sin∠BAC=![]() ,求AC和CD的长.
,求AC和CD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com