
分析 根据题目知△ABC为等腰三角形,AB=5,BC=4,分两种情况:一种是AB为腰长,一种是AB为底边,从而求出相应的sinA的值.
解答 解:当AB边为底边时,作CD⊥AB于点D,如图所示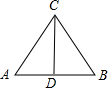
∵△ABC中为等腰三角形,AB=5,BC=4
∴CD垂直平分AB,AC=AB=4
∴AD=$\frac{5}{2}$,∠CDA=90°
∴CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{{4}^{2}-(\frac{5}{2})^{2}}=\sqrt{16-\frac{25}{4}}=\frac{\sqrt{39}}{2}$
∴sinA=$\frac{CD}{AC}=\frac{\frac{\sqrt{39}}{2}}{4}=\frac{\sqrt{39}}{8}$
当AB边为腰时,作BD⊥AC于点D,如下图所示: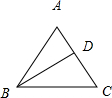
∵在等腰△ABC中,AB=5,BC=4,
∴AB=AC=5,
又∵BD⊥AC于点D,
∴∠BDA=∠BDC=90°,
设AD=x,则CD=5-x,
∵AB2-AD2=BC2-CD2
∴52-x2=42-(5-x)2
解得x=3.4
BD=$\sqrt{A{B}^{2}-A{D}^{2}}=\sqrt{{5}^{2}-3.{4}^{2}}=\sqrt{25-\frac{289}{25}}=\frac{4\sqrt{21}}{5}$
∴sinA=$\frac{BD}{AB}=\frac{\frac{4\sqrt{21}}{5}}{5}=\frac{4\sqrt{21}}{25}$.
故答案为:$\frac{\sqrt{39}}{8}$或$\frac{4\sqrt{21}}{25}$.
点评 本题考查锐角三角函数的相关知识,等腰三角形的知识,分类讨论数学思想的应用.


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:选择题
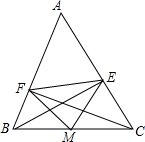 如图,在△ABC中,CF⊥AB于点F,BE⊥AC于点E,M为BC的中点,EF=5,BC=8,则△EFM的周长及图中的等腰三角形个数分别是( )
如图,在△ABC中,CF⊥AB于点F,BE⊥AC于点E,M为BC的中点,EF=5,BC=8,则△EFM的周长及图中的等腰三角形个数分别是( )| A. | 21、2 | B. | 18、3 | C. | 13、4 | D. | 13、5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
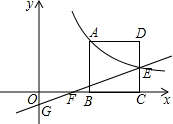 如图,正方形ABCD的顶点B、C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过顶点A(a,4)和CD边上的点E(b,2),过点E的直线l交x轴于点F,交y轴于点G(0,-1),则△OFG的面积是( )
如图,正方形ABCD的顶点B、C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象经过顶点A(a,4)和CD边上的点E(b,2),过点E的直线l交x轴于点F,交y轴于点G(0,-1),则△OFG的面积是( )| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{7}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
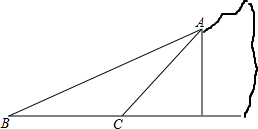 因山体滑坡,需将一段50米长的滑坡体清除,滑坡体横截面是如图所示的△ABC.测得堡坎坡面AC的坡度是1:1,滑坡体坡面AB的坡角是30°,滑坡体底宽BC=13米.
因山体滑坡,需将一段50米长的滑坡体清除,滑坡体横截面是如图所示的△ABC.测得堡坎坡面AC的坡度是1:1,滑坡体坡面AB的坡角是30°,滑坡体底宽BC=13米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
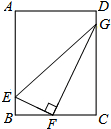 如图,矩形ABCD中,E、G为AB、CD边上的点,F为BC的中点,且BE=1,CG=4,EF⊥FG.
如图,矩形ABCD中,E、G为AB、CD边上的点,F为BC的中点,且BE=1,CG=4,EF⊥FG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com