
下列说法中正确的是( )
A. 是一个无理数
是一个无理数
B.8的立方根是±2
C.函数y= 的自变量x的取值范围是x>1
的自变量x的取值范围是x>1
D.若点P(2,a)和点Q(b,-3)关于x轴对称,则a+b的值为-5
C
【解析】
试题分析:A、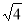 =2是有理数,故错误;B、8的立方根是2,故错误;C、函数
=2是有理数,故错误;B、8的立方根是2,故错误;C、函数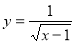 的自变量x的取值范围是x>1,正确;D、若点P(2,a)和点Q(b,-3)关于x轴对称,则有a=3、b=2,所以a+b=5,故错误;
的自变量x的取值范围是x>1,正确;D、若点P(2,a)和点Q(b,-3)关于x轴对称,则有a=3、b=2,所以a+b=5,故错误;
故选C
考点:1、无理数;2、立方根;3、函数自变量的取值范围;4、关于x轴对称的点的坐标特征
考点分析: 考点1:函数基础知识 函数的定义: 叫做二次根式。
叫做二次根式。 ”;
”; 有意义,被开方数a必须是非负数,即a≥0,由此可确定被开方数中字母的取值范围。
二次根式性质:
有意义,被开方数a必须是非负数,即a≥0,由此可确定被开方数中字母的取值范围。
二次根式性质: ≥0 (双重非负性 );
≥0 (双重非负性 ); ;
;
 ;
; 。
二次根式判定:
。
二次根式判定: ,
, 等;
等; 中,被开方数a可以是具体的一个数,也可以是代数式;
中,被开方数a可以是具体的一个数,也可以是代数式; 是一个非负数;
是一个非负数; (a≥0 )就表示a的算术平方根。
(a≥0 )就表示a的算术平方根。

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014-2015学年浙江省台州市九年级上学期第一次月考数学试卷(解析版) 题型:选择题
已知x1,x2是方程x2+6x+3=0的两实数根,则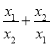 的值为( )
的值为( )
A.4 B.6 C.8 D.10
查看答案和解析>>
科目:初中数学 来源:2014-2015学年天津市九年级上学期期中考试数学试卷(解析版) 题型:填空题
若关于 的一元二次方程
的一元二次方程 有一个根为0,则
有一个根为0,则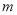 =______,另一根为________.
=______,另一根为________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省九年级上学期第一次月考数学试卷(解析版) 题型:计算题
(6分)已知函数y=kx+b的图象经过点A(- 3, - 2)及点B(1, 6).
(1)求此一次函数解析式,并画图象; (2)求函数y=2x+4图象与坐标轴围成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省九年级上学期第一次月考数学试卷(解析版) 题型:选择题
已知x=-2是一元二次方程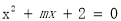 的一个解,则m的值是 ( ).
的一个解,则m的值是 ( ).
A.-3 B.3 C.0 D.0或3
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省镇江市丹徒区九年级10月调研数学试卷(解析版) 题型:计算题
(8分)在矩形 中,
中, ,
, ,点
,点 从点
从点 沿矩形的边以
沿矩形的边以 的速度经
的速度经 向
向 运动,点
运动,点 从
从 点出发沿矩形的边以
点出发沿矩形的边以 的速度经
的速度经 向
向 运动,点
运动,点 、
、 同时运动,且一点到达终点另一点也停止运动,求几秒后以
同时运动,且一点到达终点另一点也停止运动,求几秒后以 、
、 、
、 为顶点的三角形的面积等于6平方厘米?
为顶点的三角形的面积等于6平方厘米?

查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省武汉市校九年级9月联考数学试卷(解析版) 题型:解答题
(本题7分)已知关于 的方程
的方程 .
.
(1)求证:无论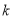 取任何实数值,方程总有实数根;
取任何实数值,方程总有实数根;
(2)若等腰三角形ABC的一边长 ,另两边长
,另两边长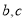 恰好是这个方程的两个根,求此三角形的周长.
恰好是这个方程的两个根,求此三角形的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com