Question

（6分）已知函数y=kx+b的图象经过点A（- 3, - 2）及点B（1, 6）．

（1）求此一次函数解析式,并画图象； （2）求函数y=2x+4图象与坐标轴围成的三角形的面积．

Answer 1

（1）一次函数解析式为y=2x+4；图象见解析；

（2）图象与两坐标轴围成的三角形面积为4；

【解析】

试题分析：（1）先利用待定系数法求出函数的解析式，再画出图形即可；

（2）先令x=0，求出y的值，再令y=0求出x的值即可得出直线与两坐标轴的交点，再根据三角形的面积公式求解即可；

试题解析：（1）∵函数y=kx+b的图象经过点A（- 3, - 2）及点B（1, 6）

∴

∴

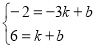
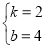
∴一次函数解析式为y=2x+4

图象如下：

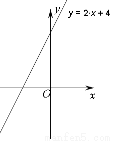
∵令x=0，则y=4；令y=0，则x=-2，

∴直线与两坐标轴的交点分别为（0，4），（-2，0），

∴函数y=-x+3的图象与两坐标轴围成的三角形面积=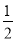×4×2=4；

考点：1、待定系数法；2、一次函数图象上点的坐标特征

考点分析： 考点1：一次函数 函数的定义：
一般地，在一个变化过程中，如果有两个自变量x与y，并且对于x的每一个确定的值，y都有唯一确定的值与其对应，那么我们就说x是自变量，y是x的函数。
对函数概念的理解，主要抓住以下三点：
①有两个变量；
②一个变量的每一个数值随着另一个变量的数值的变化而变化；
③对于自变量每一个确定的值，函数有且只有一个值与之对应。
例如：y=±x，当x=1时，y有两个对应值，所以y=±x不是函数关系。对于不同的自变量x的取值，y的值可以相同，例如，函数：y=|x|，当x=±1时，y的对应值都是1。 理解函数的概念应扣住下面三点：
（1）函数的概念由三句话组成：“两个变量”，“x的每一个值”，“y有惟一确定的值”；
（2）判断两个变量是否有函数关系不仅看它们之间是否有关系式存在，更重要地是看对于x的每一个确定的值。y是否有惟一确定的值和它对应；（3）函数不是数，它是指某一变化过程中两个变量之间的关系。 函数的表示方法：
（1）解析法：两个变量之间的关系有时可以用含有这两个变量及数学运算符号的等式来表示，这种表示方法叫做解析法．
（2）列表法：把自变量x的一系列值和函数y的对应值列成一个表格来表示函数关系，这种表示方法叫做列表法．
（3）图象法：用图象表示函数关系的方法叫做图象法． 函数的判定：
①判断两个变量是否有函数关系，不仅看他们之间是否有关系式存在，更重要的是看对于x的每个确定的值，y是否有唯一确定的值和他对应。
②函数不是数，他是指某一变化过程中两个变量之间的关系。 试题属性

• 题型：
• 难度：
• 考核：
• 年级：