
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上. 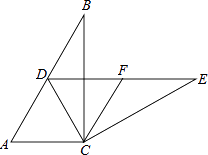
(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
【答案】
(1)解:∵在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,
∴AC=DC,∠A=60°,
∴△ADC是等边三角形,
∴∠ACD=60°,
∴n的值是60
(2)解:四边形ACFD是菱形;
理由:∵∠DCE=∠ACB=90°,F是DE的中点,
∴FC=DF=FE,
∵∠CDF=∠A=60°,
∴△DFC是等边三角形,
∴DF=DC=FC,
∵△ADC是等边三角形,
∴AD=AC=DC,
∴AD=AC=FC=DF,
∴四边形ACFD是菱形
【解析】(1)利用旋转的性质得出AC=CD,进而得出△ADC是等边三角形,即可得出∠ACD的度数;(2)利用直角三角形的性质得出FC=DF,进而得出AD=AC=FC=DF,即可得出答案.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】已知如图,射线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF。
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC∶∠OFC的值是否随之变化?若变化,找出变化规律;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某县政府为了迎接“八一”建军节,加强军民共建活动,计划从花园里拿出1430盆甲种花卉和1220盆乙种花卉,搭配成A、B两种园艺造型共20个,在城区内摆放,以增加节日气氛,已知搭配A、B两种园艺造型各需甲、乙两种花卉数如表所示:(单位:盆)
(1)某校某年级一班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮忙设计出来.
(2)如果搭配及摆放一个A造型需要的人力是8人次,搭配及摆放一个B造型需要的人力是11人次,哪种方案使用人力的总人次数最少,请说明理由.
造型数量花 | A | B |
甲种 | 80 | 50 |
乙种 | 40 | 90 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解一元二次不等式 ![]() .
.
请按照下面的步骤,完成本题的解答.
解: ![]() 可化为
可化为 ![]() .
.
(1)依据“两数相乘,同号得正”,可得不等式组①![]() 或不等式组②________.
或不等式组②________.
(2)解不等式组①,得________.
(3)解不等式组②,得________.
(4)一元二次不等式 ![]() 的解集为________.
的解集为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.

(1)求证:AE=2CE;
(2)连接CD,请判断△BCD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+bx+c与x轴交于点A(1,0),B(3,0),与y轴交于点C. 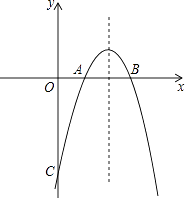
(1)求抛物线的解析式;
(2)设点P在该抛物线上滑动,则满足S△PAB=1的点P有几个?求出所有点P的坐标;
(3)在该抛物线的对称轴上存在点M,使得△MAC的周长最小,求出这个点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某地一座抛物线形拱桥,桥拱在竖直平面内,与水平桥面相交于A、B两点,拱桥最高点C到AB的距离为4m,AB=12m,D、E为拱桥底部的两点,且DE∥AB,点E到直线AB的距离为5m,则DE的长为m. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F。

(1)求证:△ABE≌△CAD;(2)求∠BFD的度数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com