
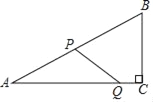
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬��A=30�㣬AB=8����P�ӵ�A������������AB��BC���յ�C�˶�����AB����ÿ��8����λ���ȵ��ٶ��˶�����BC����ÿ��2����λ���ȵ��ٶ��˶�����Q�ӵ�C��������CA������ÿ��![]() ����λ���ȵ��ٶ��˶�������ͬʱ����������Pֹͣʱ����QҲ��ֹ֮ͣ�����P�˶���ʱ��Ϊt�룮
����λ���ȵ��ٶ��˶�������ͬʱ����������Pֹͣʱ����QҲ��ֹ֮ͣ�����P�˶���ʱ��Ϊt�룮
��1�����߶�AQ�ij������ú�t�Ĵ���ʽ��ʾ��
��2������P��AB�����˶�ʱ����PQ���ABC��һ�ߴ�ֱʱt��ֵ��
��3�����APQ�����ΪS����S��t�ĺ�����ϵʽ��
��4������APQ����PQΪ���ĵ���������ʱ��ֱ��д��t��ֵ��
���𰸡���1��4![]() ��
��![]() t����2������P��AB�����˶�ʱ��PQ���ABC��һ�ߴ�ֱʱt��ֵ��t=0��
t����2������P��AB�����˶�ʱ��PQ���ABC��һ�ߴ�ֱʱt��ֵ��t=0��![]() ��
��![]() ����3��S��t�ĺ�����ϵʽΪ��S=
����3��S��t�ĺ�����ϵʽΪ��S=![]() ����4��t��ֵΪ
����4��t��ֵΪ![]() ��
��![]() ��
��
����������������1�����ݹ��ɶ������AC�ij���Ȼ����AQ=AC-CQ��⼴�ɣ�
��2������P��AB�����˶�ʱ��PQ���ABC��һ�ߴ�ֱ���������������Q��C����P��A��ʱ��PQ��BC����PQ��ABʱ����PQ��ACʱ���ֱ���⼴����
��3����P��AB����ʱ����0��t��1����PG��AC��G����P�ڱ�BC��ʱ����1��t��3���ֱ���������ε���������Ľ���ʽ������
��4������APQ����PQΪ���ĵ���������ʱ��������������ٵ�P�ڱ�AB��ʱ����PG��AC��G����AG=GQ���з���������ڵ�P�ڱ�AC��ʱ�� AQ=PQ�����ݹ��ɶ������.
��⣺��1����ͼ1��
Rt��ABC�У���A=30�㣬AB=8��
��BC=![]() AB=4��
AB=4��
��AC=![]() ��
��
������ã�CQ=![]() t��
t��
��AQ=4![]() ��
��![]() t��
t��
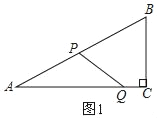
��2������P��AB�����˶�ʱ��PQ���ABC��һ�ߴ�ֱ�������������
�ٵ�Q��C����P��A��ʱ��PQ��BC����ʱt=0��
�ڵ�PQ��ABʱ����ͼ2��
��AQ=4![]() ��
��![]() t��AP=8t����A=30�㣬
t��AP=8t����A=30�㣬
��cos30��=![]() ��
��
��![]() ��
��
t=![]() ��
��
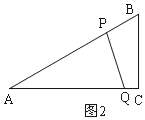
�۵�PQ��ACʱ����ͼ3��
��AQ=4![]() ��
��![]() t��AP=8t����A=30�㣬
t��AP=8t����A=30�㣬
��cos30��=![]() ��
��
��![]()
t=![]() ��
��
��������������P��AB�����˶�ʱ��PQ���ABC��һ�ߴ�ֱʱt��ֵ��t=0��![]() ��
��![]() ��
��
��3�������������
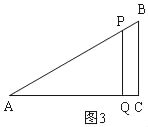
�ٵ�P��AB����ʱ����0��t��1����ͼ4����PG��AC��G��
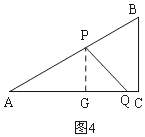
�ߡ�A=30�㣬AP=8t����AGP=90�㣬
��PG=4t��
��S��APQ=![]() AQPG=
AQPG=![]() ��4
��4![]() ��
��![]() t��4t=��2
t��4t=��2![]() t2+8
t2+8![]() t��
t��
�ڵ�P�ڱ�BC��ʱ����1��t��3����ͼ5��
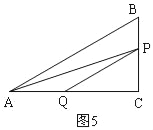
������ã�PB=2��t��1����
��PC=4��2��t��1��=��2t+6��
��S��APQ=![]() AQPC=
AQPC=![]() ��4
��4![]() ��
��![]() t������2t+6��=
t������2t+6��=![]() t2
t2![]() ��
��
����������S��t�ĺ�����ϵʽΪ��S=![]() ��
��
��4������APQ����PQΪ���ĵ���������ʱ�������������
�ٵ�P�ڱ�AB��ʱ����ͼ6��
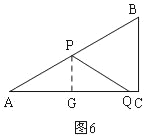
AP=PQ����PG��AC��G����AG=GQ��
�ߡ�A=30�㣬AP=8t����AGP=90�㣬
��PG=4t��
��AG=4![]() t��
t��
��AQ=2AG�ã�4![]() ��
��![]() t=8
t=8![]() t��t=
t��t=![]() ��
��
�ڵ�P�ڱ�AC��ʱ����ͼ7��AQ=PQ��
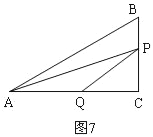
Rt��PCQ�У��ɹ��ɶ����ã�CQ2+CP2=PQ2��
��![]() ��
��
t=![]() ��
��![]() ���ᣩ��
���ᣩ��
����������t��ֵΪ![]() ��
��![]() ��
��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������п������ؿ���Ŀ֮һ��������ijѧУΪ�˽������꼶ѧ�������������������������ȡ���־��꼶ѧ����������IJ��Գɼ���Ϊһ����������A��B��C��D�ĸ��ȼ�����ͳ�ƣ��Ƴ������²�������ͳ��ͼ����˵����A����8�֩�10�֣�B����7�֩�7.9�֣�C����6�֩�6.9�֣�D����1�֩�5.9�֣�
����������Ϣ������������⣺
��1��������ͳ��ͼ�У�C��Ӧ�����ε�Բ�Ľ����� ���ȣ�
��2����ȫ����ͳ��ͼ��
��3������ȡѧ��������������Գɼ�����λ���������� ���ȼ���
��4����У���꼶��300��ѧ�������������������Գɼ��ﵽA����ѧ���ж����ˣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC����ǡ�ACD��ƽ����CP���ABCƽ����BP���ڵ�P������BPC=40�������CAP�Ķ����ǣ� ��
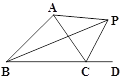
A. 30���� B. 40���� C. 50���� D. 60��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������x�ķ���x2-2��m��1��x��m2=0.
��1����mȡ��ֵʱ������������ʵ������
��2��Ϊmѡȡһ�����ʵ�������ʹ��������������ȵ�ʵ��������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
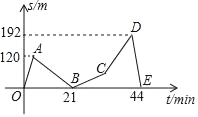
����Ŀ���ְֺ�С���ݳ�ȥ�����ɽ�����������Ĵ����㣨�˰��ž飩������ɽ�£��ְ���С���ȳ���6min��Ȼ�������ϣ����ְֳ���24minʱ���������绰���м��£�Ҫ��������ȥ�����ǰְֺ�С�����ϰ�ԭ·��ɽ���أ��м�ӵ绰����ʱ�䲻�ƣ������˷���ɽ�µ�ʱ�����4min������С���Ͱְָ����ϡ���ɽ���ٶ��Ǿ��ȵģ���ɽ������С���Ͱְ�֮��ľ���s����λ��m������С������ʱ��t����λ��min���ĺ���ͼ����ͼ������ͼ����Ϣ����������⣺
��1��С���Ͱְ���ɽʱ���ٶȸ��Ƕ��٣�
��2������ְ���ɽʱCD�εĺ�������ʽ��
��3����ɽ���ص����£�������೬��120m�ͻ������������˻��������ʱ���ж��ٷ��ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1��![]() ��
��
��2����x��2a��2��a��2a��x����
��3��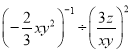 ��
��
��4��������ֵ��![]() ������m��
������m��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ABC�У�CD��AB��D����BD : AD : CD��2 : 3 : 4��
��1����˵����ABC�ǵ��������Σ�
��2����֪S��ABC��40cm2����ͼ2������M�ӵ�B������ÿ��2cm���ٶ����߶�BA���A �˶���ͬʱ����N�ӵ�A������ÿ��1cm�ٶ����߶�AC���C�˶���������һ�㵽���յ�ʱ�����˶���ֹͣ. ���M�˶���ʱ��Ϊt���룩��
������DMN�ı���BCƽ�У���t��ֵ��
������E�DZ�AC���е㣬���ڵ�M�˶��Ĺ����У���MDE�ܷ��Ϊ���������Σ����ܣ����t��ֵ�������ܣ���˵�����ɣ�
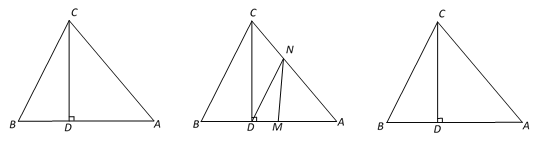
ͼ1 ͼ2 ����ͼ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=10��AC=8��BC=6���Ա�AB���е�OΪԲ�ģ�����Բ��AC���У���P��Q�ֱ��DZ�BC�Ͱ�Բ�ϵĶ��㣬����PQ����PQ�������ֵ����Сֵ�ĺ��ǣ�������
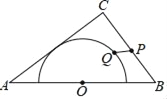
A. 9 B. 10 C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��P�ǡ�O��һ�㣬����P����O������һ����AB�����ǰ�PAPB��ֵ��Ϊ��P���ڡ�O������ֵ��
��1����O�İ뾶Ϊ6��OP=4��
����ͼ1������PǡΪ��AB���е㣬���P���ڡ�O������ֵ��Ϊ_____��
���жϵ���AB��λ�øı�ʱ����P���ڡ�O������ֵ���Ƿ�Ϊ��ֵ�����Ƕ�ֵ��֤����Ľ��ۣ������Ƕ�ֵ�����P���ڡ�0������ֵ����ȡֵ��Χ��
��2������O�İ뾶Ϊr��OP=d����ο���1����˼·���ú�r��d��ʽ�ӱ�ʾ��P���ڡ�O������ֵ��������ֵ����ȡֵ��Χ_____��
��3����ƽ��ֱ������ϵxOy�У�C��1��0������C�İ뾶Ϊ3������ֱ��y=![]() x+b�ϴ��ڵ�P��ʹ�õ�P���ڡ�C������ֵ��Ϊ6����ֱ��д��b��ȡֵ��Χ_____��
x+b�ϴ��ڵ�P��ʹ�õ�P���ڡ�C������ֵ��Ϊ6����ֱ��д��b��ȡֵ��Χ_____��
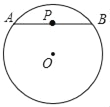
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com