
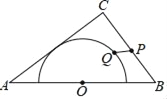
【题目】如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是( )
A. 9 B. 10 C. ![]() D.
D. ![]()
【答案】A
【解析】
如图,设⊙O与AC相切于点E,连接OE,作OP1⊥BC垂足为P1交⊙O于Q1,
此时垂线段OP1最短,P1Q1最小值为OP1﹣OQ1,求出OP1,如图当Q2在AB边上时,P2
与B重合时,P2Q2最大值=5+3=8,由此不难解决问题.
如图,设⊙O与AC相切于点E,连接OE,作OP1⊥BC垂足为P1交⊙O于Q1,
此时垂线段OP1最短,P1Q1最小值为OP1﹣OQ1,
∵AB=10,AC=8,BC=6,
∴AB2=AC2+BC2,
∴∠C=90°,
∵∠OP1B=90°,
∴OP1∥AC
∵AO=OB,
∴P1C=P1B,
∴OP1=![]() AC=4,
AC=4,
∴P1Q1最小值为OP1﹣OQ1=1,
如图,当Q2在AB边上时,P2与B重合时,P2Q2经过圆心,经过圆心的弦最长,
P2Q2最大值=5+3=8,
∴PQ长的最大值与最小值的和是9.
故选:A.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BD平分∠ABC,
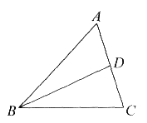
(1)作图:作BC边的垂直平分线分别交BC,BD于点E,F(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,连接CF,若∠A=60°,∠ABD=24°,求∠ACF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
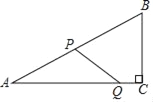
【题目】如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=8,点P从点A出发,沿折线AB﹣BC向终点C运动,在AB上以每秒8个单位长度的速度运动,在BC上以每秒2个单位长度的速度运动,点Q从点C出发,沿CA方向以每秒![]() 个单位长度的速度运动,两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.
个单位长度的速度运动,两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.
(1)求线段AQ的长;(用含t的代数式表示)
(2)当点P在AB边上运动时,求PQ与△ABC的一边垂直时t的值;
(3)设△APQ的面积为S,求S与t的函数关系式;
(4)当△APQ是以PQ为腰的等腰三角形时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,P是AB上的动点(P异于A、B),过点P的直线截△ABC,使截得的三角形与△ABC相似,我们不妨称这种直线为过点P的△ABC的相似线,简记为P(![]() ),(
),(![]() 为自然数)
为自然数)
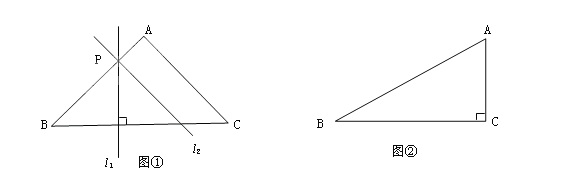
(1)如图①,∠A=90°,∠B=∠C,当BP=2PA时,P(![]() )、P(
)、P(![]() )都是过点P的△ABC的相似线(其中
)都是过点P的△ABC的相似线(其中![]() ⊥BC,
⊥BC,![]() ∥AC),此外还有_______条.
∥AC),此外还有_______条.
(2)如图②,∠C=90°,∠B=30°,当![]() _____时,P(
_____时,P(![]() )截得的三角形面积为△ABC面积的
)截得的三角形面积为△ABC面积的![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
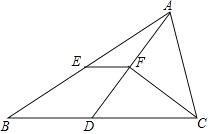
【题目】如图,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CF交AD于点F,点E是AB的中点,连结EF.
(1)求证:EF∥BC;
(2)若四边形BDFE的面积为3,求△AEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次学生夏令营活动,有小学生、初中生、高中生和大学生参加,共200人,各类学生人数比例见扇形统计图.
(1)参加这次夏令营活动的初中生共有多少人?
(2)活动组织者号召参加这次夏令营活动的所有学生为贫困学生捐款.结果小学生每人
捐款 5 元,初中生每人捐款 10 元,高中生每人捐款 15 元,大学生每人捐款 20 元.问平均 每人捐款是多少元?
(3)在(2)的条件下,把每个学生的捐款数额(以元为单位)——记录下来,则在这组数据中,众数是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
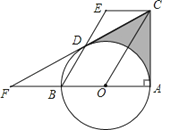
【题目】如图,AB是⊙O的直径,∠BAC=90°,四边形EBOC是平行四边形,EB交⊙O于点D,连接CD并延长交AB的延长线于点F.
(1)求证:CF是⊙O的切线;
(2)若∠F=30°,EB=4,求图中阴影部分的面积(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
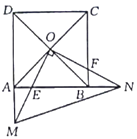
【题目】如图,正方形![]() 的对角线交于点
的对角线交于点![]() 点
点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上(
上(![]() )且
)且![]() ,
,![]() ,
,![]() 的延长线交于点
的延长线交于点![]() ,
,![]() ,
,![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() .
.
(1)求证:![]() .
.
(2)若正方形![]() 的边长为4,
的边长为4,![]() 为
为![]() 的中点,求
的中点,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x与抛物线y=x2﹣x﹣3交于A、B两点,点P是抛物线上的一个动点,过点P作直线PQ⊥x轴,交直线y=x于点Q,设点P的横坐标为m,则线段PQ的长度随m的增大而减小时m的取值范围是( )

A. m<﹣1或m>![]() B. m<﹣1或
B. m<﹣1或![]() <m<3 C. m<﹣1或m>3 D. m<﹣1或1<m<3
<m<3 C. m<﹣1或m>3 D. m<﹣1或1<m<3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com