
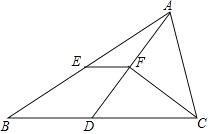
【题目】如图,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CF交AD于点F,点E是AB的中点,连结EF.
(1)求证:EF∥BC;
(2)若四边形BDFE的面积为3,求△AEF的面积.
【答案】(1)见解析;(2)1
【解析】
(1)依据等腰三角形的性质,即可得到F是AD的中点,再根据三角形中位线定理,即可得到EF∥BC;
(2)依据EF是△ABD的中位线,即可得到EF∥BC,EF:BD=1:2,进而得到S△DEF:S△DEB=1:2,再依据F是AD的中点,即可得出S△DEF=S△AEF=1.
(1)∵DC=AC,CF平分∠ACD,
∴F是AD的中点,
又∵E是AB的中点,
∴EF是△ABD的中位线,
∴EF∥BC;
(2)∵EF是△ABD的中位线,
∴EF∥BC,EF:BD=1:2,
如图,连接DE,则S△DEF:S△DEB=1:2,
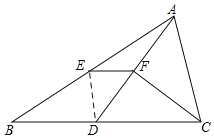
又∵四边形BDFE的面积为3,
∴S△DEF=1,
又∵F是AD的中点,
∴S△DEF=S△AEF=1.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
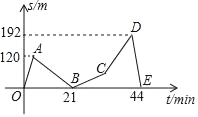
【题目】爸爸和小芳驾车去郊外登山,欣赏美丽的达子香(兴安杜鹃),到了山下,爸爸让小芳先出发6min,然后他再追赶,待爸爸出发24min时,妈妈来电话,有急事,要求立即回去.于是爸爸和小芳马上按原路下山返回(中间接电话所用时间不计),二人返回山下的时间相差4min,假设小芳和爸爸各自上、下山的速度是均匀的,登山过程中小芳和爸爸之间的距离s(单位:m)关于小芳出发时间t(单位:min)的函数图象如图,请结合图象信息解答下列问题:
(1)小芳和爸爸上山时的速度各是多少?
(2)求出爸爸下山时CD段的函数解析式;
(3)因山势特点所致,二人相距超过120m就互相看不见,求二人互相看不见的时间有多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,CD⊥AB于D,且BD : AD : CD=2 : 3 : 4,
(1)试说明△ABC是等腰三角形;
(2)已知S△ABC=40cm2,如图2,动点M从点B出发以每秒2cm的速度沿线段BA向点A 运动,同时动点N从点A出发以每秒1cm速度沿线段AC向点C运动,当其中一点到达终点时整个运动都停止. 设点M运动的时间为t(秒),
①若△DMN的边与BC平行,求t的值;
②若点E是边AC的中点,问在点M运动的过程中,△MDE能否成为等腰三角形?若能,求出t的值;若不能,请说明理由.
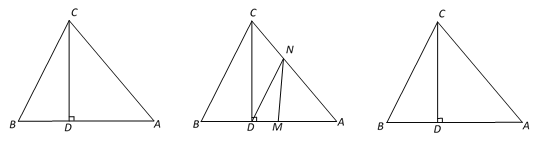
图1 图2 备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为创建“书香校园”,购置了一批图书,已知购买科普类图书花费10000元,购买文学类图书花费9000元,其中科普类图书平均每本的价格比文学类图书平均每本的价格贵5元,且购买科普类图书的数量与购买文学类图书的数量相等.求科普类图书平均每本的价格.
查看答案和解析>>
科目:初中数学 来源: 题型:
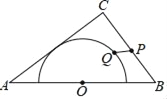
【题目】如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是( )
A. 9 B. 10 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100个)为优秀.下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
1号 | 2号 | 3号 | 4号 | 5号 | 总成绩 | |
甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
经统计发现两班总成绩相等,只好将数据中的其他信息作为参考.根据要求回答下列问题:
(1)计算两班的优秀率;
(2)求两班比赛数据的中位数;
(3)求两班比赛数据的方差;
(4)根据以上三条信息,你认为应该把冠军奖状发给哪一个班级?简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”
用今天的话说,大意是:如图,![]() 是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门
是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门![]() 位于
位于![]() 的中点,南门
的中点,南门![]() 位于
位于![]() 的中点,出东门15步的
的中点,出东门15步的![]() 处有一树木,求出南门多少步恰好看到位于
处有一树木,求出南门多少步恰好看到位于![]() 处的树木(即点
处的树木(即点![]() 在直线
在直线![]() 上)?请你计算
上)?请你计算![]() 的长为__________步.
的长为__________步.

查看答案和解析>>
科目:初中数学 来源: 题型:
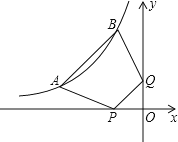
【题目】如图,点A(a,1)、B(﹣1,b)都在双曲线y=![]() 上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是( )
上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是( )
A.y=x B.y=x+1 C.y=x+2 D.y=x+3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com