
【题目】《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”
用今天的话说,大意是:如图,![]() 是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门
是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门![]() 位于
位于![]() 的中点,南门
的中点,南门![]() 位于
位于![]() 的中点,出东门15步的
的中点,出东门15步的![]() 处有一树木,求出南门多少步恰好看到位于
处有一树木,求出南门多少步恰好看到位于![]() 处的树木(即点
处的树木(即点![]() 在直线
在直线![]() 上)?请你计算
上)?请你计算![]() 的长为__________步.
的长为__________步.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
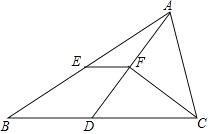
【题目】如图,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CF交AD于点F,点E是AB的中点,连结EF.
(1)求证:EF∥BC;
(2)若四边形BDFE的面积为3,求△AEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
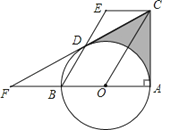
【题目】如图,AB是⊙O的直径,∠BAC=90°,四边形EBOC是平行四边形,EB交⊙O于点D,连接CD并延长交AB的延长线于点F.
(1)求证:CF是⊙O的切线;
(2)若∠F=30°,EB=4,求图中阴影部分的面积(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() ,
,![]() ,
,![]() ,AD、BE相交于点M,连接CM.
,AD、BE相交于点M,连接CM.![]() 求证:
求证:![]() ;
;![]() 求
求![]() 的度数
的度数![]() 用含
用含![]() 的式子表示
的式子表示![]() ;
;![]() 如图2,当
如图2,当![]() 时,点P、Q分别为AD、BE的中点,分别连接CP、CQ、PQ,判断
时,点P、Q分别为AD、BE的中点,分别连接CP、CQ、PQ,判断![]() 的形状,并加以证明.
的形状,并加以证明.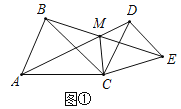
查看答案和解析>>
科目:初中数学 来源: 题型:
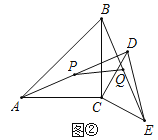
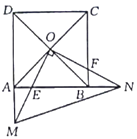
【题目】如图,正方形![]() 的对角线交于点
的对角线交于点![]() 点
点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上(
上(![]() )且
)且![]() ,
,![]() ,
,![]() 的延长线交于点
的延长线交于点![]() ,
,![]() ,
,![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() .
.
(1)求证:![]() .
.
(2)若正方形![]() 的边长为4,
的边长为4,![]() 为
为![]() 的中点,求
的中点,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图甲是一个大长方形剪去一个小长方形后形成的图形,已知动点P以每秒2cm的速度沿图甲的边框按从B→C→D→E→F→A的路径移动,相应的△ABP的面积S与时间t之间的关系如图乙中的图象表示.若AB=6cm,试回答下列问题
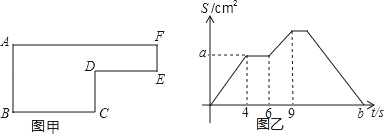
(1)图甲中的BC长是多少?
(2)图乙中的a是多少?
(3)图甲中的图形面积的多少?
(4)图乙中的b是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若点P(a,b)在函数y=![]() 的图象上,将以a为二次项系数,b为一次项系数构造的二次函数y=ax2+bx称为函数y=
的图象上,将以a为二次项系数,b为一次项系数构造的二次函数y=ax2+bx称为函数y=![]() 的一个“派生函数”.例如:点(2,
的一个“派生函数”.例如:点(2, ![]() )在函数y=
)在函数y=![]() 的图象上,则函数y=2x2+
的图象上,则函数y=2x2+ ![]() 称为函数y=
称为函数y=![]() 的一个“派生函数”.现给出以下两个命题:
的一个“派生函数”.现给出以下两个命题:
(1)存在函数y=![]() 的一个“派生函数”,其图象的对称轴在y轴的右侧
的一个“派生函数”,其图象的对称轴在y轴的右侧
(2)函数y=![]() 的所有“派生函数”的图象都经过同一点,下列判断正确的是( )
的所有“派生函数”的图象都经过同一点,下列判断正确的是( )
A. 命题(1)与命题(2)都是真命题
B. 命题(1)与命题(2)都是假命题
C. 命题(1)是假命题,命题(2)是真命题
D. 命题(1)是真命题,命题(2)是假命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com