
【题目】如图甲是一个大长方形剪去一个小长方形后形成的图形,已知动点P以每秒2cm的速度沿图甲的边框按从B→C→D→E→F→A的路径移动,相应的△ABP的面积S与时间t之间的关系如图乙中的图象表示.若AB=6cm,试回答下列问题
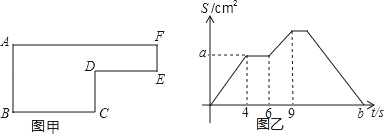
(1)图甲中的BC长是多少?
(2)图乙中的a是多少?
(3)图甲中的图形面积的多少?
(4)图乙中的b是多少?
【答案】(1)8cm; (2)24cm2;(3)60cm2;(4)17秒.
【解析】
(1)根据题意得:动点P在BC上运动的时间是4秒,又由动点的速度,可得BC的长;
(2)由(1)可得BC的长,又由AB=6cm,可以计算出△ABP的面积,计算可得a的值;
(3)分析图形可得,甲中的图形面积等于AB×AF﹣CD×DE,根据图象求出CD和DE的长,代入数据计算可得答案;
(4)计算BC+CD+DE+EF+FA的长度,又由P的速度,计算可得b的值.
(1)动点P在BC上运动时,对应的时间为0到4秒,易得:BC=2cm/秒×4秒=8cm;
故图甲中的BC长是8cm;
(2)由(1)可得,BC=8cm,则:a=![]() ×BC×AB=24cm2;
×BC×AB=24cm2;
图乙中的a是24cm2;
(3)由图可得:CD=2×2=4cm,DE=2×3=6cm,
则AF=BC+DE=14cm,又由AB=6cm,
则甲图的面积为AB×AF﹣CD×DE=60cm2,
图甲中的图形面积为60cm2;
(4)根据题意,动点P共运动了BC+CD+DE+EF+FA=8+4+6+2+14=34cm,
其速度是2cm/秒,则b=![]() =17秒,
=17秒,
图乙中的b是17秒.


科目:初中数学 来源: 题型:
【题目】爸爸和小芳驾车去郊外登山,欣赏美丽的达子香(兴安杜鹃),到了山下,爸爸让小芳先出发6min,然后他再追赶,待爸爸出发24min时,妈妈来电话,有急事,要求立即回去.于是爸爸和小芳马上按原路下山返回(中间接电话所用时间不计),二人返回山下的时间相差4min,假设小芳和爸爸各自上、下山的速度是均匀的,登山过程中小芳和爸爸之间的距离s(单位:m)关于小芳出发时间t(单位:min)的函数图象如图,请结合图象信息解答下列问题:
(1)小芳和爸爸上山时的速度各是多少?
(2)求出爸爸下山时CD段的函数解析式;
(3)因山势特点所致,二人相距超过120m就互相看不见,求二人互相看不见的时间有多少分钟?
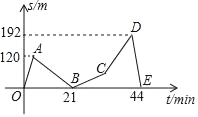
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100个)为优秀.下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
1号 | 2号 | 3号 | 4号 | 5号 | 总成绩 | |
甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
经统计发现两班总成绩相等,只好将数据中的其他信息作为参考.根据要求回答下列问题:
(1)计算两班的优秀率;
(2)求两班比赛数据的中位数;
(3)求两班比赛数据的方差;
(4)根据以上三条信息,你认为应该把冠军奖状发给哪一个班级?简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”
用今天的话说,大意是:如图,![]() 是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门
是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门![]() 位于
位于![]() 的中点,南门
的中点,南门![]() 位于
位于![]() 的中点,出东门15步的
的中点,出东门15步的![]() 处有一树木,求出南门多少步恰好看到位于
处有一树木,求出南门多少步恰好看到位于![]() 处的树木(即点
处的树木(即点![]() 在直线
在直线![]() 上)?请你计算
上)?请你计算![]() 的长为__________步.
的长为__________步.

查看答案和解析>>
科目:初中数学 来源: 题型:
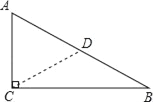
【题目】如图,在Rt△ABC中,∠C=90°,AC=![]() AB.求证:∠B=30°.
AB.求证:∠B=30°.
请填空完成下列证明.
证明:如图,作Rt△ABC的斜边上的中线CD,
则 CD=![]() AB=AD ( ).
AB=AD ( ).
∵AC=![]() AB,
AB,
∴AC=CD=AD 即△ACD是等边三角形.
∴∠A= °.
∴∠B=90°﹣∠A=30°.
查看答案和解析>>
科目:初中数学 来源: 题型:
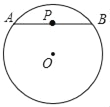
【题目】P是⊙O内一点,过点P作⊙O的任意一条弦AB,我们把PAPB的值称为点P关于⊙O的“幂值”
(1)⊙O的半径为6,OP=4.
①如图1,若点P恰为弦AB的中点,则点P关于⊙O的“幂值”为_____;
②判断当弦AB的位置改变时,点P关于⊙O的“幂值”是否为定值,若是定值,证明你的结论;若不是定值,求点P关于⊙0的“幂值”的取值范围;
(2)若⊙O的半径为r,OP=d,请参考(1)的思路,用含r、d的式子表示点P关于⊙O的“幂值”或“幂值”的取值范围_____;
(3)在平面直角坐标系xOy中,C(1,0),⊙C的半径为3,若在直线y=![]() x+b上存在点P,使得点P关于⊙C的“幂值”为6,请直接写出b的取值范围_____.
x+b上存在点P,使得点P关于⊙C的“幂值”为6,请直接写出b的取值范围_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,将两个完全相同的三角形纸片 ABC 和 DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)如图2,固定△ABC,使△DEC 绕点 C 旋转,当点 D 恰好落 在 AB 边上时,
①填空:线段 DE 与 AC 的位置关系是 ;
②设△BDC 的面积为 S1,△AEC 的面积为 S2,求证:S1=S2
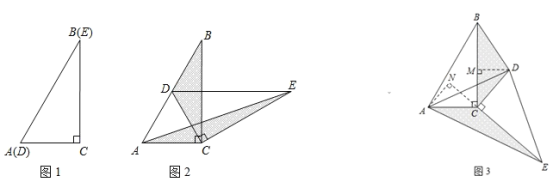
(2)当△DEC 绕点 C 旋转到如图 3 所示的位置时,小明猜想(1) 中 S1 与 S2 的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE 边上的高,请你证明小明的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(a,1)、B(﹣1,b)都在双曲线y=![]() 上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是( )
上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是( )
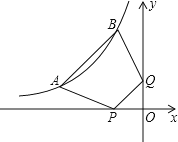
A.y=x B.y=x+1 C.y=x+2 D.y=x+3
查看答案和解析>>
科目:初中数学 来源: 题型:
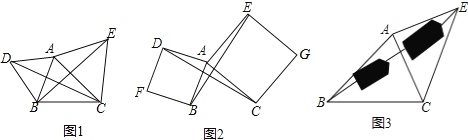
【题目】(1)作图发现:
如图1,已知![]() ,小涵同学以
,小涵同学以![]() 、
、![]() 为边向
为边向![]() 外作等边
外作等边![]() 和等边
和等边![]() ,连接
,连接![]() ,
,![]() .这时他发现
.这时他发现![]() 与
与![]() 的数量关系是 .
的数量关系是 .
(2)拓展探究:
如图2,已知![]() ,小涵同学以
,小涵同学以![]() 、
、![]() 为边向外作正方形
为边向外作正方形![]() 和正方形
和正方形![]() ,连接
,连接![]() ,
,![]() ,试判断
,试判断![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
(3)解决问题
如图3,要测量池塘两岸相对的两点![]() ,
,![]() 的距离,已经测得
的距离,已经测得![]() ,
,![]() ,
,![]() 米,
米,![]() ,则
,则![]() 米.
米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com