
����Ŀ��P�ǡ�O��һ�㣬����P����O������һ����AB�����ǰ�PAPB��ֵ��Ϊ��P���ڡ�O������ֵ��
��1����O�İ뾶Ϊ6��OP=4��
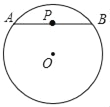
����ͼ1������PǡΪ��AB���е㣬���P���ڡ�O������ֵ��Ϊ_____��
���жϵ���AB��λ�øı�ʱ����P���ڡ�O������ֵ���Ƿ�Ϊ��ֵ�����Ƕ�ֵ��֤����Ľ��ۣ������Ƕ�ֵ�����P���ڡ�0������ֵ����ȡֵ��Χ��
��2������O�İ뾶Ϊr��OP=d����ο���1����˼·���ú�r��d��ʽ�ӱ�ʾ��P���ڡ�O������ֵ��������ֵ����ȡֵ��Χ_____��
��3����ƽ��ֱ������ϵxOy�У�C��1��0������C�İ뾶Ϊ3������ֱ��y=![]() x+b�ϴ��ڵ�P��ʹ�õ�P���ڡ�C������ֵ��Ϊ6����ֱ��д��b��ȡֵ��Χ_____��
x+b�ϴ��ڵ�P��ʹ�õ�P���ڡ�C������ֵ��Ϊ6����ֱ��д��b��ȡֵ��Χ_____��
���𰸡���1����20���ڵ���AB��λ�øı�ʱ����P���ڡ�O������ֵ��Ϊ��ֵ��֤������������2����P���ڡ�O������ֵ��Ϊr2��d2����3����3![]() ��b��
��b��![]() .
.
������������⡿��1������ͼ1��ʾ������OA��OB��OP���ɵ��������ε����ߺ�һ�����ʵõ���PBOΪֱ�������Σ�Ȼ�����ݹ��ɶ��������PB�ij���Ȼ��������ֵ�Ķ�����⼴�ɣ�
�ڹ���P����O����A��B����OP������AA�䡢BB������֤����APA���ס�B��PB���������������ε����ʵõ�PAPB=PA��PB���Ӷ��ó����ۣ�
��2������OP������P��AB��OP����ԲO��A��B���㣮�ɵ������������ߺ�һ�����ʿ�֪AP=PB��Ȼ����Rt��APO�У����ݹ��ɶ�����֪AP2=OA2-OP2��Ȼ��d��r����ɵõ�����Ĵ𰸣�
��3������C��CP��AB�������OP�Ľ���ʽ��Ȼ����ֱ��AB��OP�Ľ���ʽ���õ���P�����꣬Ȼ��������Բ����ֵΪ6���뾶Ϊ4�����d��ֵ���ٽ�������ľ��빫ʽ�ɵõ�����b�ķ��̣��Ӷ������b�ļ�ֵ���ݴ˼���ȷ����b��ȡֵ��Χ��
����⡿��1������ͼ1��ʾ������OA��OB��OP��

��OA=OB��PΪAB���е㣬
��OP��AB��
������PBO�У��ɹ��ɶ����ã�PB=![]() =2
=2![]() ��
��
��PA=PB=2![]() ��
��
���O������ֵ��=2![]() ��2
��2![]() =20��
=20��
�ʴ�Ϊ��20��
�ڵ���AB��λ�øı�ʱ����P���ڡ�O������ֵ��Ϊ��ֵ��֤�����£�
��ͼ��ABΪ��O�й���P������һ���ң��Ҳ���OP��ֱ������P����O����A��B����OP������AA�䡢BB�䣬
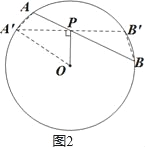
���ڡ�O�У���AA��P=��B��BP����APA��=��BPB�䣬
���APA���ס�B��PB��
��![]() ��
��
��PAPB=PA��PB��=20��
�൱��AB��λ�øı�ʱ����P���ڡ�O������ֵ��Ϊ��ֵ��
��2����ͼ3��ʾ������OP������P��AB��OP����ԲO��A��B������
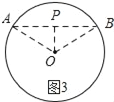
��AO=OB��PO��AB��
��AP=PB��
���P���ڡ�O������ֵ��=APPB=PA2��
��Rt��APO��AP2=OA2��OP2=r2��d2��
����ڡ�O������ֵ��=r2��d2��
�ʴ�Ϊ����P���ڡ�O������ֵ��Ϊr2��d2��
��3����ͼ4��ʾ������C��CP��AB��
 ��
��
��CP��AB��AB�Ľ���ʽΪy=![]() x+b��
x+b��
��ֱ��CP�Ľ���ʽΪy=��![]() x+
x+![]() ��
��
����AB��CP����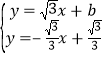 ��
��
���P����������![]() ��
��![]() b��
b��![]() +
+![]() b����
b����
�ߵ�P���ڡ�C������ֵ��Ϊ6��
��r2��d2=6��
��d2=3��������![]() ��
��![]() b��2+��
b��2+��![]() +
+![]() b��2=3��
b��2=3��
�����ã�b2+2![]() b��9=0��
b��9=0��
���b=��3![]() ��b=
��b=![]() ��
��
��b��ȡֵ��Χ�ǩ�3![]() ��b��
��b��![]() ��
��
�ʴ�Ϊ����3![]() ��b��
��b��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
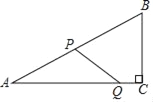
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬��A=30�㣬AB=8����P�ӵ�A������������AB��BC���յ�C�˶�����AB����ÿ��8����λ���ȵ��ٶ��˶�����BC����ÿ��2����λ���ȵ��ٶ��˶�����Q�ӵ�C��������CA������ÿ��![]() ����λ���ȵ��ٶ��˶�������ͬʱ����������Pֹͣʱ����QҲ��ֹ֮ͣ�����P�˶���ʱ��Ϊt�룮
����λ���ȵ��ٶ��˶�������ͬʱ����������Pֹͣʱ����QҲ��ֹ֮ͣ�����P�˶���ʱ��Ϊt�룮
��1�����߶�AQ�ij������ú�t�Ĵ���ʽ��ʾ��
��2������P��AB�����˶�ʱ����PQ���ABC��һ�ߴ�ֱʱt��ֵ��
��3�����APQ�����ΪS����S��t�ĺ�����ϵʽ��
��4������APQ����PQΪ���ĵ���������ʱ��ֱ��д��t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
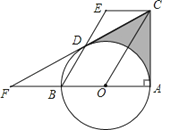
����Ŀ����ͼ��AB�ǡ�O��ֱ������BAC=90�����ı���EBOC��ƽ���ı��Σ�EB����O�ڵ�D������CD���ӳ���AB���ӳ����ڵ�F��
��1����֤��CF�ǡ�O�����ߣ�
��2������F=30����EB=4����ͼ����Ӱ���ֵ����������������ź�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
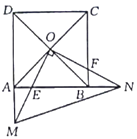
����Ŀ����ͼ��������![]() �ĶԽ��߽��ڵ�
�ĶԽ��߽��ڵ�![]() ��
��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �ϣ�
�ϣ�![]() ����
����![]() ��
��![]() ��
��![]() ���ӳ��߽��ڵ�
���ӳ��߽��ڵ�![]() ��
��![]() ��
��![]() ���ӳ��߽��ڵ�
���ӳ��߽��ڵ�![]() ������
������![]() .
.
��1����֤��![]() .
.
��2����������![]() �ı߳�Ϊ4��
�ı߳�Ϊ4��![]() Ϊ
Ϊ![]() ���е㣬��
���е㣬��![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�����μ�ȥһ��С�����κ��γɵ�ͼ�Σ���֪����P��ÿ��2cm���ٶ���ͼ�ı߿�B��C��D��E��F��A��·���ƶ�����Ӧ����ABP�����S��ʱ��t֮��Ĺ�ϵ��ͼ���е�ͼ���ʾ����AB=6cm���Իش���������
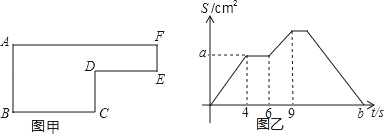
��1��ͼ���е�BC���Ƕ��٣�
��2��ͼ���е�a�Ƕ��٣�
��3��ͼ���е�ͼ������Ķ��٣�
��4��ͼ���е�b�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
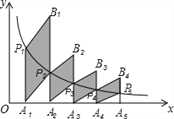
����Ŀ����ͼ���ֱ������������y��![]() ��ͼ���ϵĵ�P1(1��y1)��P2(2��y2)����Pn(n��yn)����x��Ĵ��ߣ�����ֱ�ΪA1��A2������An��������A1P2��A2P3����,An-1Pn����������A1P1��A1P2Ϊһ���ڱ�һ��ƽ���ı���A1P1B1P2����A 2P2��A2P3Ϊһ���ڱ�һ��ƽ���ı���A2P2B2P3����B2����������____.�������ƣ����Bn����������_______.(����ú�n����ʽ��ʾ)
��ͼ���ϵĵ�P1(1��y1)��P2(2��y2)����Pn(n��yn)����x��Ĵ��ߣ�����ֱ�ΪA1��A2������An��������A1P2��A2P3����,An-1Pn����������A1P1��A1P2Ϊһ���ڱ�һ��ƽ���ı���A1P1B1P2����A 2P2��A2P3Ϊһ���ڱ�һ��ƽ���ı���A2P2B2P3����B2����������____.�������ƣ����Bn����������_______.(����ú�n����ʽ��ʾ)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��![]() ���㣬��
���㣬��![]() ���ڵ�
���ڵ�![]() ����
����![]() ����������ߵĽ���ʽΪ________��
����������ߵĽ���ʽΪ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=x��������y=x2��x��3����A��B���㣬��P���������ϵ�һ�����㣬����P��ֱ��PQ��x�ᣬ��ֱ��y=x�ڵ�Q�����P�ĺ�����Ϊm�����߶�PQ�ij�����m���������Сʱm��ȡֵ��Χ�ǣ�������

A. m����1��m��![]() B. m����1��
B. m����1��![]() ��m��3 C. m����1��m��3 D. m����1��1��m��3
��m��3 C. m����1��m��3 D. m����1��1��m��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
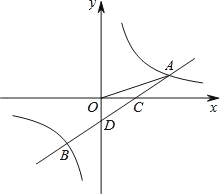
����Ŀ����ͼ��һ�κ���y=ax��1��ͼ���뷴��������y=![]() ��ͼ����A��B���㣬��x�ύ�ڵ�C����y�ύ�ڵ�D����֪OA=
��ͼ����A��B���㣬��x�ύ�ڵ�C����y�ύ�ڵ�D����֪OA=![]() ��tan��AOC=
��tan��AOC=![]() ��
��
��1����a��k��ֵ����B�����ꣻ
��2���۲�ͼ����ֱ��д������ʽax��1��![]() �Ľ⼯��
�Ľ⼯��
��3����y���ϴ���һ��P��ʹ����PDC����ODC���ƣ��������P������꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com