
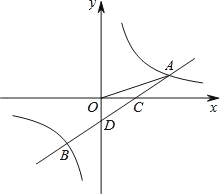
【题目】如图,一次函数y=ax﹣1的图象与反比例函数y=![]() 的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知OA=
的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知OA=![]() ,tan∠AOC=
,tan∠AOC=![]() .
.
(1)求a,k的值及点B的坐标;
(2)观察图象,请直接写出不等式ax﹣1≥![]() 的解集;
的解集;
(3)在y轴上存在一点P,使得△PDC与△ODC相似,请你求出P点的坐标.
【答案】(1)a=![]() ,k=3, B(-
,k=3, B(-![]() ,-2) (2) ﹣
,-2) (2) ﹣![]() ≤x<0或x≥3;(3) (0,
≤x<0或x≥3;(3) (0,![]() )或(0,0)
)或(0,0)
【解析】
1)过A作AE⊥x轴,交x轴于点E,在Rt△AOE中,根据tan∠AOC的值,设AE=x,得到OE=3x,再由OA的长,利用勾股定理列出关于x的方程,求出方程的解得到x的值,确定出A坐标,将A坐标代入一次函数解析式求出a的值,代入反比例解析式求出k的值,联立一次函数与反比例函数解析式求出B的坐标;
(2)由A与B交点横坐标,根据函数图象确定出所求不等式的解集即可;
(3)显然P与O重合时,满足△PDC与△ODC相似;当PC⊥CD,即∠PCD=![]() 时,满足三角形PDC与三角形CDO相等,利用同角的余角相等得到一对角相等,再由一对直角相等得到三角形PCO与三角形CDO相似,由相 似得比例,根据OD,OC的长求出OP的长,即可确定出P的坐标.
时,满足三角形PDC与三角形CDO相等,利用同角的余角相等得到一对角相等,再由一对直角相等得到三角形PCO与三角形CDO相似,由相 似得比例,根据OD,OC的长求出OP的长,即可确定出P的坐标.
解:(1)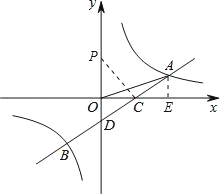
过A作AE⊥x轴,交x轴于点E,
在Rt△AOE中,OA=![]() ,tan∠AOC=
,tan∠AOC=![]() ,
,
设AE=x,则OE=3x,
根据勾股定理得:OA2=OE2+AE2,即10=9x2+x2,
解得:x=1或x=﹣1(舍去),
∴OE=3,AE=1,即A(3,1),
将A坐标代入一次函数y=ax﹣1中,得:1=3a﹣1,即a=![]() ,
,
将A坐标代入反比例解析式得:1=![]() ,即k=3,
,即k=3,
联立一次函数与反比例解析式得: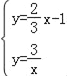 ,
,
消去y得:![]() x﹣1=
x﹣1=![]() ,
,
解得:x=﹣![]() 或x=3,
或x=3,
将x=﹣![]() 代入得:y=﹣1﹣1=﹣2,即B(﹣
代入得:y=﹣1﹣1=﹣2,即B(﹣![]() ,﹣2);
,﹣2);
(2)由A(3,1),B(﹣![]() ,﹣2),
,﹣2),
根据图象得:不等式![]() x﹣1≥
x﹣1≥![]() 的解集为﹣
的解集为﹣![]() ≤x<0或x≥3;
≤x<0或x≥3;
(3)显然P与O重合时,△PDC∽△ODC;
当PC⊥CD,即∠PCD=90°时,∠PCO+∠DCO=90°,
∵∠PCD=∠COD=90°,∠PCD=∠CDO,
∴△PDC∽△CDO,
∵∠PCO+∠CPO=90°,
∴∠DCO=∠CPO,
∵∠POC=∠COD=90°,
∴△PCO∽△CDO,
∴![]() =
=![]() ,
,
对于一次函数解析式y=![]() x﹣1,令x=0,得到y=﹣1;令y=0,得到x=
x﹣1,令x=0,得到y=﹣1;令y=0,得到x=![]() ,
,
∴C(![]() ,0),D(0,﹣1),即OC=
,0),D(0,﹣1),即OC=![]() ,OD=1,
,OD=1,
∴![]() =
=![]() ,即OP=
,即OP=![]() ,
,
此时P坐标为(0,![]() ),
),
综上,满足题意P的坐标为(0,![]() )或(0,0).
)或(0,0).


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
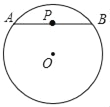
【题目】P是⊙O内一点,过点P作⊙O的任意一条弦AB,我们把PAPB的值称为点P关于⊙O的“幂值”
(1)⊙O的半径为6,OP=4.
①如图1,若点P恰为弦AB的中点,则点P关于⊙O的“幂值”为_____;
②判断当弦AB的位置改变时,点P关于⊙O的“幂值”是否为定值,若是定值,证明你的结论;若不是定值,求点P关于⊙0的“幂值”的取值范围;
(2)若⊙O的半径为r,OP=d,请参考(1)的思路,用含r、d的式子表示点P关于⊙O的“幂值”或“幂值”的取值范围_____;
(3)在平面直角坐标系xOy中,C(1,0),⊙C的半径为3,若在直线y=![]() x+b上存在点P,使得点P关于⊙C的“幂值”为6,请直接写出b的取值范围_____.
x+b上存在点P,使得点P关于⊙C的“幂值”为6,请直接写出b的取值范围_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011山东济南,22,3分)如图1,△ABC中,∠C=90°,∠ABC=30°,AC=m,延长CB至点D,使BD=AB.
①求∠D的度数;
②求tan75°的值.
(2)如图2,点M的坐标为(2,0),直线MN与y轴的正半轴交于点N,∠OMN=75°.求直线MN的函数表达式.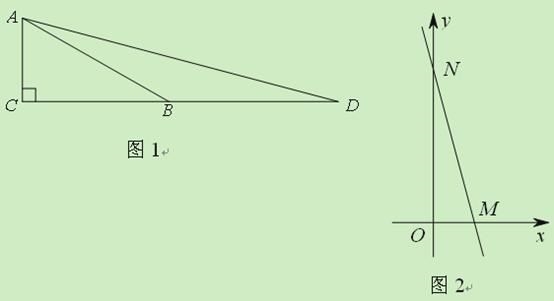
查看答案和解析>>
科目:初中数学 来源: 题型:
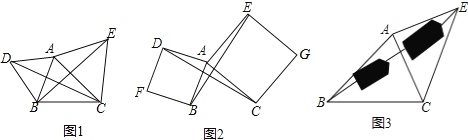
【题目】(1)作图发现:
如图1,已知![]() ,小涵同学以
,小涵同学以![]() 、
、![]() 为边向
为边向![]() 外作等边
外作等边![]() 和等边
和等边![]() ,连接
,连接![]() ,
,![]() .这时他发现
.这时他发现![]() 与
与![]() 的数量关系是 .
的数量关系是 .
(2)拓展探究:
如图2,已知![]() ,小涵同学以
,小涵同学以![]() 、
、![]() 为边向外作正方形
为边向外作正方形![]() 和正方形
和正方形![]() ,连接
,连接![]() ,
,![]() ,试判断
,试判断![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
(3)解决问题
如图3,要测量池塘两岸相对的两点![]() ,
,![]() 的距离,已经测得
的距离,已经测得![]() ,
,![]() ,
,![]() 米,
米,![]() ,则
,则![]() 米.
米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明平时喜欢玩“开心消消乐”游戏,本学期在学校组织的几次数学反馈性测试中,小明的数学成绩如下表:
月份 |
|
|
|
|
|
|
成绩(分) |
|
|
|
| ··· | ··· |
(1)以月份为x轴,成绩为y轴,根据上表提供的数据在平面直角坐标系中描点;
(2)观察(1)中所描点的位置关系,猜想![]() 与
与![]() 之间的的函数关系,并求出所猜想的函数表达式;
之间的的函数关系,并求出所猜想的函数表达式;
(3)若小明继续沉溺于“开心消消乐“游戏,照这样的发展趋势,请你估计元月(此时![]() )份的考试中小明的数学成绩,并用一句话对小明提出一些建议.
)份的考试中小明的数学成绩,并用一句话对小明提出一些建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
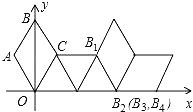
【题目】如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1,先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2017次,点B的落点依次为B1,B2,B3,…,则B2017的坐标为( )
A. (1345,0) B. (1345.5,![]() ) C. (1345,
) C. (1345,![]() ) D. (1345.5,0)
) D. (1345.5,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市正在举行文化艺术节活动,一商店抓住商机,决定购进甲,乙两种艺术节纪念品.若购进甲种纪念品4件,乙种纪念品3件,需要550元,若购进甲种纪念品5件,乙种纪念品6件,需要800元.
(1)求购进甲、乙两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共80件,其中甲种纪念品的数量不少于60件.考虑到资金周转,用于购买这80件纪念品的资金不能超过7100元,那么该商店共有几种进货方案7
(3)若销售每件甲种纪含晶可获利润20元,每件乙种纪念品可获利润30元.在(2)中的各种进货方案中,若全部销售完,哪一种方案获利最大?最大利利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一段路基的横断面是直角梯形,如图1,已知原来坡面的坡角α的正弦值为0.6,现不改变土石方量,全部利用原有土石方进行坡面改造,使坡度变小,达到如右下图2的技术要求.试求出改造后坡面的坡度是多少?
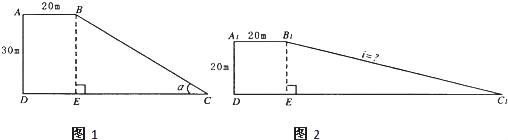
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com