【题目】如图，直线y=x与抛物线y=x2﹣x﹣3交于A、B两点，点P是抛物线上的一个动点，过点P作直线PQ⊥x轴，交直线y=x于点Q，设点P的横坐标为m，则线段PQ的长度随m的增大而减小时m的取值范围是（ ）
A. m＜﹣1或m＞
B. m＜﹣1或＜m＜3 C. m＜﹣1或m＞3 D. m＜﹣1或1＜m＜3
名师指导期末冲刺卷系列答案科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=10，AC=8，BC=6，以边AB的中点O为圆心，作半圆与AC相切，点P，Q分别是边BC和半圆上的动点，连接PQ，则PQ长的最大值与最小值的和是（ ）
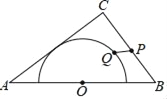
A. 9 B. 10 C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
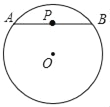
【题目】P是⊙O内一点，过点P作⊙O的任意一条弦AB，我们把PAPB的值称为点P关于⊙O的“幂值”
（1）⊙O的半径为6，OP=4．
①如图1，若点P恰为弦AB的中点，则点P关于⊙O的“幂值”为_____；
②判断当弦AB的位置改变时，点P关于⊙O的“幂值”是否为定值，若是定值，证明你的结论；若不是定值，求点P关于⊙0的“幂值”的取值范围；
（2）若⊙O的半径为r，OP=d，请参考（1）的思路，用含r、d的式子表示点P关于⊙O的“幂值”或“幂值”的取值范围_____；
（3）在平面直角坐标系xOy中，C（1，0），⊙C的半径为3，若在直线y=
x+b上存在点P，使得点P关于⊙C的“幂值”为6，请直接写出b的取值范围_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，点
的坐标为
，
的面积是
．
求点
的坐标；
求过点、
、的抛物线的解析式；
在中抛物线的对称轴上是否存在点
，使
的周长最小？若存在，求出点的坐标；若不存在，请说明理由；
在中
轴下方的抛物线上是否存在一点
，过点作轴的垂线，交直线
于点
，线段
把分成两个三角形，使其中一个三角形面积与四边形
面积比为
？若存在，求出点的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点A（a，1）、B（﹣1，b）都在双曲线y=
上，点P、Q分别是x轴、y轴上的动点，当四边形PABQ的周长取最小值时，PQ所在直线的解析式是（ ）
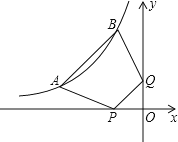
A．y=x B.y=x+1 C.y=x+2 D.y=x+3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1所示的图形，像我们常见的符号——箭号．我们不妨把这样图形叫做“箭头四角形”．
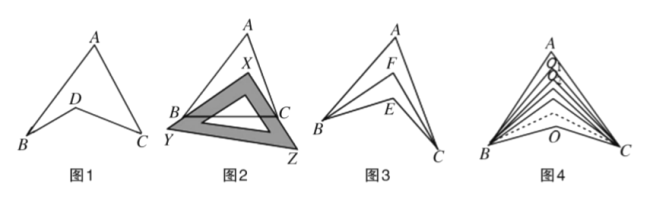
探究：
（1）观察“箭头四角形”，试探究
与
、
、
之间的关系，并说明理由；
应用：
（2）请你直接利用以上结论，解决以下两个问题：
①如图2，把一块三角尺
放置在
上，使三角尺的两条直角边
、
恰好经过点
、
，若
，则
；
②如图3，
、
的2等分线（即角平分线）
、
相交于点
，若
，
，求
的度数；
拓展：
（3）如图4，
，
分别是
、
的2020等分线（
），它们的交点从上到下依次为
、
、
、…、
．已知
，
，则
度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（2011山东济南，22，3分）如图1，△ABC中，∠C=90°，∠ABC=30°，AC=m，延长CB至点D，使BD=AB．
①求∠D的度数；
②求tan75°的值．
（2）如图2，点M的坐标为（2，0），直线MN与y轴的正半轴交于点N，∠OMN=75°．求直线MN的函数表达式．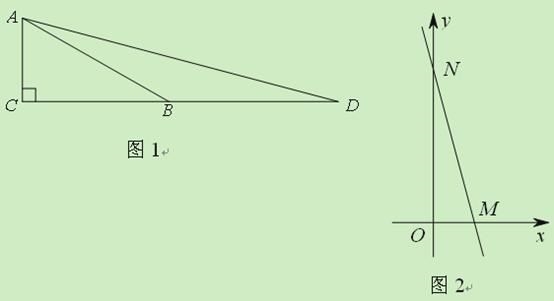
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某市正在举行文化艺术节活动，一商店抓住商机，决定购进甲，乙两种艺术节纪念品．若购进甲种纪念品4件，乙种纪念品3件，需要550元，若购进甲种纪念品5件，乙种纪念品6件，需要800元．
（1）求购进甲、乙两种纪念品每件各需多少元？
（2）若该商店决定购进这两种纪念品共80件，其中甲种纪念品的数量不少于60件．考虑到资金周转，用于购买这80件纪念品的资金不能超过7100元，那么该商店共有几种进货方案7
（3）若销售每件甲种纪含晶可获利润20元，每件乙种纪念品可获利润30元．在（2）中的各种进货方案中，若全部销售完，哪一种方案获利最大？最大利利润多少元？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
