
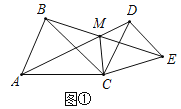
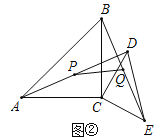
【题目】如图1,![]() ,
,![]() ,
,![]() ,AD、BE相交于点M,连接CM.
,AD、BE相交于点M,连接CM.![]() 求证:
求证:![]() ;
;![]() 求
求![]() 的度数
的度数![]() 用含
用含![]() 的式子表示
的式子表示![]() ;
;![]() 如图2,当
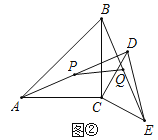
如图2,当![]() 时,点P、Q分别为AD、BE的中点,分别连接CP、CQ、PQ,判断
时,点P、Q分别为AD、BE的中点,分别连接CP、CQ、PQ,判断![]() 的形状,并加以证明.
的形状,并加以证明.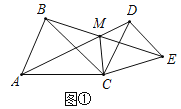
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() 为等腰直角三角形,证明见解析.
为等腰直角三角形,证明见解析.
【解析】
分析(1)由CA=CB,CD=CE,∠ACB=∠DCE=α,利用SAS即可判定△ACD≌△BCE;
(2)根据△ACD≌△BCE,得出∠CAD=∠CBE,再根据∠AFC=∠BFH,即可得到∠AMB=∠ACB=α;
(3)先根据SAS判定△ACP≌△BCQ,再根据全等三角形的性质,得出CP=CQ,∠ACP=∠BCQ,最后根据∠ACB=90°即可得到∠PCQ=90°,进而得到△PCQ为等腰直角三角形.
![]() 如图1,
如图1,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
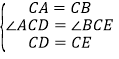 ,
,
![]() ≌
≌![]()
![]() ;
;
![]() 如图1,
如图1,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() 中,
中,![]() ,
,
![]() ,
,
![]() 中,
中,![]() ;
;
![]() 为等腰直角三角形.
为等腰直角三角形.
证明:如图2,由![]() 可得,
可得,![]() ,
,
![]() ,BE的中点分别为点P、Q,
,BE的中点分别为点P、Q,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
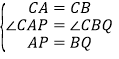 ,
,
![]() ≌
≌![]() ,
,
![]() ,且
,且![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
![]() 为等腰直角三角形.
为等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,点
,点![]() 为直线
为直线![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 重合),以
重合),以![]() 为腰作等腰直角
为腰作等腰直角![]() ,使
,使![]() ,连接
,连接![]() .
.
(1)观察猜想
如图1,当点![]() 在线段
在线段![]() 上时,
上时,
①![]() 与
与![]() 的位置关系为__________;
的位置关系为__________;
②![]() 之间的数量关系为___________(提示:可证
之间的数量关系为___________(提示:可证![]() )
)

(2)数学思考
如图2,当点![]() 在线段
在线段![]() 的延长线上时,(1)中的①、②结论是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明;
的延长线上时,(1)中的①、②结论是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明;
(3)拓展延伸
如图3,当点![]() 在线段
在线段![]() 的延长线时,将
的延长线时,将![]() 沿线段
沿线段![]() 翻折,使点
翻折,使点![]() 与点
与点![]() 重合,连接
重合,连接![]() ,若
,若![]() ,请直接写出线段
,请直接写出线段![]() 的长.(提示:做
的长.(提示:做![]() 于
于![]() ,做
,做![]() 于
于![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为创建“书香校园”,购置了一批图书,已知购买科普类图书花费10000元,购买文学类图书花费9000元,其中科普类图书平均每本的价格比文学类图书平均每本的价格贵5元,且购买科普类图书的数量与购买文学类图书的数量相等.求科普类图书平均每本的价格.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100个)为优秀.下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
1号 | 2号 | 3号 | 4号 | 5号 | 总成绩 | |
甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
经统计发现两班总成绩相等,只好将数据中的其他信息作为参考.根据要求回答下列问题:
(1)计算两班的优秀率;
(2)求两班比赛数据的中位数;
(3)求两班比赛数据的方差;
(4)根据以上三条信息,你认为应该把冠军奖状发给哪一个班级?简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近期江苏省各地均发布“雾霾”黄色预警,我市某口罩厂商生产一种新型口罩产品,每件制造成本为18元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系满足下表.
销售单价x(元/件) | … | 20 | 25 | 30 | 40 | … |
每月销售量y(万件) | … | 60 | 50 | 40 | 20 | … |
(1)请你从所学过的一次函数、二次函数和反比例函数三个模型中确定哪种函数能比较恰当地表示y与x的变化规律,并直接写出y与x之间的函数关系式为__________;
(2)当销售单价为多少元时,厂商每月获得的利润为440万元?
(3)如果厂商每月的制造成本不超过540万元,那么当销售单价为多少元时,厂商每月获得的利润最大?最大利润为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”
用今天的话说,大意是:如图,![]() 是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门
是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门![]() 位于
位于![]() 的中点,南门
的中点,南门![]() 位于
位于![]() 的中点,出东门15步的
的中点,出东门15步的![]() 处有一树木,求出南门多少步恰好看到位于
处有一树木,求出南门多少步恰好看到位于![]() 处的树木(即点
处的树木(即点![]() 在直线
在直线![]() 上)?请你计算
上)?请你计算![]() 的长为__________步.
的长为__________步.

查看答案和解析>>
科目:初中数学 来源: 题型:
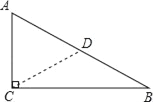
【题目】如图,在Rt△ABC中,∠C=90°,AC=![]() AB.求证:∠B=30°.
AB.求证:∠B=30°.
请填空完成下列证明.
证明:如图,作Rt△ABC的斜边上的中线CD,
则 CD=![]() AB=AD ( ).
AB=AD ( ).
∵AC=![]() AB,
AB,
∴AC=CD=AD 即△ACD是等边三角形.
∴∠A= °.
∴∠B=90°﹣∠A=30°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,将两个完全相同的三角形纸片 ABC 和 DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)如图2,固定△ABC,使△DEC 绕点 C 旋转,当点 D 恰好落 在 AB 边上时,
①填空:线段 DE 与 AC 的位置关系是 ;
②设△BDC 的面积为 S1,△AEC 的面积为 S2,求证:S1=S2
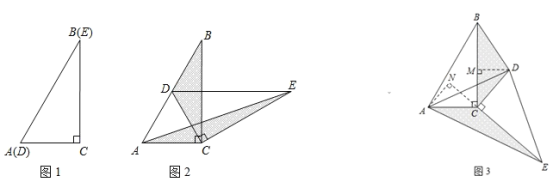
(2)当△DEC 绕点 C 旋转到如图 3 所示的位置时,小明猜想(1) 中 S1 与 S2 的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE 边上的高,请你证明小明的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=﹣x+1与抛物线y=![]() x2+bx+c交于A(0,1),B两点,B点纵坐标为10,抛物线的顶点为C.
x2+bx+c交于A(0,1),B两点,B点纵坐标为10,抛物线的顶点为C.
(1)求b,c的值;
(2)判断△ABC的形状并说明理由;
(3)点D、E分别为线段AB、BC上任意一点,连接CD,取CD的中点F,连接AF,EF.当四边形ADEF为平行四边形时,求平行四边形ADEF的周长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com