
【题目】如图,在△ABC中,∠B=50°,点D为边AB的中点,点E在边AC上,将△ADE沿DE折叠,使得点A恰好落在BC的延长线上的点F处,DF与AC交于点O,连结CD,则下列结论一定正确的是( )
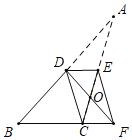
A. CE=EFB. ∠BDF=90°
C. △EOD和△COF的面积相等D. ∠BDC=∠CEF+∠A
【答案】A
【解析】
由折叠的性质和等腰三角形的判定得出选项A正确;由等腰三角形的性质和三角形内角和定理得出选项B不正确;由DE∥BC判断选项C不正确;由三角形的外角性质判断选项D不正确.
解:∵点D为边AB的中点,
∴AD=BD,由折叠知,FD=AD,∠DFE=∠A,
∴BD=FD,
∴∠B=∠DFB,
∵∠EFC=∠DFB+∠DFE,∠ECF=∠B+∠A,
∴∠EFC=∠ECF,
∴CE=EF,故A正确;
∵BD=FD,
∴∠B=∠DFB=50°,
∴∠BDF=180°﹣2×50°=80°,故B不正确;
由折叠知,EF=AE,
∴AE=CE,
∵BD=CD,
∴DE是△ABC的中位线,
∴DE∥BC,AB=2DE,
∴△DCE的面积=△DEF的面积,△CFD的面积=△CFE的面积,
当DE=CF时,△EOD和△COF的面积相等,故C不正确;
∵∠BDC=∠DCE+∠A,
当CD∥EF时,∠DCE=∠CEF,∠BDC=∠CEF+∠A,
故D不正确;
故选:A.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=![]() ,BD=2,求OE的长.
,BD=2,求OE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
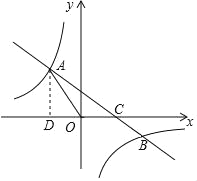
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (n≠0)的图象交于第二、四象限内的A、B两点,与x轴交于点C,点B 坐标为(m,﹣1),AD⊥x轴,且AD=3,tan∠AOD=
(n≠0)的图象交于第二、四象限内的A、B两点,与x轴交于点C,点B 坐标为(m,﹣1),AD⊥x轴,且AD=3,tan∠AOD=![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)点E是x轴上一点,且△AOE是等腰三角形,请直接写出所有符合条件的E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(1,5),直线l1:y=x,直线l2过原点且与x轴正半轴成60°夹角,在l1上有一动点M,在l2上有一动点N,连接AM、MN,则AM+MN的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小强洗漱时的侧面示意图,洗漱台(矩形ABCD)靠墙摆放,高AD=80cm,宽AB=48cm,小强身高166cm,下半身FG=100cm.洗漱时下半身与地面成80°角(即∠FGK=80°),身体前倾成125°角(即∠EFG=125°),脚与洗漱台的距离GC=15cm(点D、C、G、K在同一直线上).
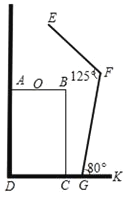
(1)求此时小强头部E点与地面DK的距离;
(2)小强希望他的头部E点恰好在洗漱盆AB的中点O的正上方,他应向前或后退多少(结果精确到0.1cm,参考数据:cos80°≈0.17,sin80°≈0.98,![]() ≈1.41)?
≈1.41)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人在山坡坡脚C处测得一座建筑物定点A的仰角为60°,沿山坡向上走到P处再测得该建筑物顶点A的仰角为45°.已知BC=60m,山坡的坡比为1:2.
(1)求该建筑物的高度(即AB的长,结果保留根号);
(2)求此人所在位置点P的铅直高度(即PD的长,结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【操作发现】
如图①,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.

(1)请按要求画图:将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′;
(2)在(1)所画图形中,∠AB′B= .
【问题解决】
如图②,在等边三角形ABC中,AC=7,点P在△ABC内,且∠APC=90°,∠BPC=120°,求△APC的面积.
小明同学通过观察、分析、思考,对上述问题形成了如下想法:
想法一:将△APC绕点A按顺时针方向旋转60°,得到△AP′B,连接PP′,寻找PA,PB,PC三条线段之间的数量关系;
想法二:将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,连接PP′,寻找PA,PB,PC三条线段之间的数量关系.
…
请参考小明同学的想法,完成该问题的解答过程.(一种方法即可)
【灵活运用】
如图③,在四边形ABCD中,AE⊥BC,垂足为E,∠BAE=∠ADC,BE=CE=2,CD=5,AD=kAB(k为常数),求BD的长(用含k的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017四川省内江市)如图,已知直线l1∥l2,l1、l2之间的距离为8,点P到直线l1的距离为6,点Q到直线l2的距离为4,PQ=![]() ,在直线l1上有一动点A,直线l2上有一动点B,满足AB⊥l2,且PA+AB+BQ最小,此时PA+BQ=______.
,在直线l1上有一动点A,直线l2上有一动点B,满足AB⊥l2,且PA+AB+BQ最小,此时PA+BQ=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 了解“孝感市初中生每天课外阅读书籍时间的情况”最适合的调查方式是全面调查
B. 甲乙两人跳绳各10次,其成绩的平均数相等,![]() ,则甲的成绩比乙稳定
,则甲的成绩比乙稳定
C. 三张分别画有菱形,等边三角形,圆的卡片,从中随机抽取一张,恰好抽到中心对称图形卡片的概率是![]()
D. “任意画一个三角形,其内角和是![]() ”这一事件是不可能事件
”这一事件是不可能事件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com