
【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.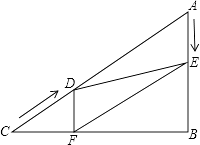
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
【答案】
(1)
证明:∵直角△ABC中,∠C=90°﹣∠A=30°.
∵CD=4t,AE=2t,
又∵在直角△CDF中,∠C=30°,
∴DF= ![]() CD=2t,
CD=2t,
∴DF=AE
(2)
解:∵DF∥AB,DF=AE,
∴四边形AEFD是平行四边形,
当AD=AE时,四边形AEFD是菱形,
即60﹣4t=2t,
解得:t=10,
即当t=10时,AEFD是菱形
(3)
解:当t= ![]() 时△DEF是直角三角形(∠EDF=90°);
时△DEF是直角三角形(∠EDF=90°);
当t=12时,△DEF是直角三角形(∠DEF=90°).理由如下:
当∠EDF=90°时,DE∥BC.
∴∠ADE=∠C=30°
∴AD=2AE
∵CD=4t,
∴DF=2t=AE,
∴AD=4t,
∴4t+4t=60,
∴t= ![]() 时,∠EDF=90°.
时,∠EDF=90°.
当∠DEF=90°时,DE⊥EF,
∵四边形AEFD是平行四边形,
∴AD∥EF,
∴DE⊥AD,
∴△ADE是直角三角形,∠ADE=90°,
∵∠A=60°,
∴∠DEA=30°,
∴AD= ![]() AE,
AE,
AD=AC﹣CD=60﹣4t,AE=DF= ![]() CD=2t,
CD=2t,
∴60﹣4t=t,
解得t=12.
综上所述,当t= ![]() 时△DEF是直角三角形(∠EDF=90°);当t=12时,△DEF是直角三角形(∠DEF=90°)
时△DEF是直角三角形(∠EDF=90°);当t=12时,△DEF是直角三角形(∠DEF=90°)
【解析】(1)利用t表示出CD以及AE的长,然后在直角△CDF中,利用直角三角形的性质求得DF的长,即可证明;(2)易证四边形AEFD是平行四边形,当AD=AE时,四边形AEFD是菱形,据此即可列方程求得t的值;(3)分两种情况讨论即可求解.


 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,BC=2,E是AB的中点,直线![]() 平行于直线EC,且直线
平行于直线EC,且直线![]() 与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线
与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线![]() 上, 则DF的长为_____
上, 则DF的长为_____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,∠C=90°,点D,E分别是边AC,BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在线段AB上,如图①,且∠α=50°,则∠1+∠2=; 
(2)若点P在斜边AB上运动,如图②,则∠α、∠1、∠2之间的关系为; 
(3)如图③,若点P在斜边BA的延长线上运动(CE<CD),请直接写出∠α、∠1、∠2之间的关系:; 
(4)若点P运动到△ABC形外(只需研究图④情形),则∠α、∠1、∠2之间有何关系?并说明理由. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com