
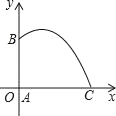
【题目】改革开放后,不少农村用上了自动喷灌设备.如图所示,AB表示水管,在B处有一个自动旋转的喷水头,一瞬间喷出的水是抛物线状,建立如图所示的直角坐标系后,抛物线的表达式为y=﹣![]() x2+2x+
x2+2x+![]() .
.
(1)当x=1时,喷出的水离地面多高?
(2)你能求出水的落地点距水管底部A的最远距离吗?
(3)水管有多高?
科目:初中数学 来源: 题型:
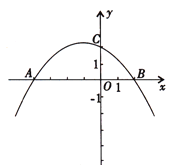
【题目】如图,抛物线![]() (
(![]() ≠0)与
≠0)与![]() 轴交于A(-4,0),B(2,0),与
轴交于A(-4,0),B(2,0),与![]() 轴交与点C(0,2).
轴交与点C(0,2).
(1)求抛物线的解析式;
(2)若点D为该抛物线上的一个动点,且在直线AC上方,当以A,C,D为顶点的三角形面积最大时,求点D的坐标及此时三角形的面积;
查看答案和解析>>
科目:初中数学 来源: 题型:
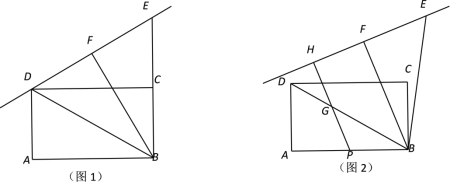
【题目】已知,在矩形ABCD中,BC=2,连接BD,把△ABD绕点B顺时针旋转后得到△FBE,旋转角度小于360°.
(1)如图1,当点E在BC的延长线上,且直线EF过点D,求AB的长.
(2)若AB=4,如图2,取AB边的中点P,过点P作直线EF的垂线PH,垂足为H.
① 若PH交线段BD于点G,当△BPG为等腰三角形时,求BG的长;
② 直接写出PH长的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,BC=6,AB=10.点Q与点B在AC的同侧,且AQ⊥AC.

(1)如图1,点Q不与点A重合,连结CQ交AB于点P.设AQ=x,AP=y,求y关于x的函数解析式,并写出自变量x的取值范围;
(2)是否存在点Q,使△PAQ与△ABC相似,若存在,求AQ的长;若不存在,请说明理由;
(3)如图2,过点B作BD⊥AQ,垂足为D.将以点Q为圆心,QD为半径的圆记为⊙Q.若点C到⊙Q上点的距离的最小值为8,求⊙Q的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
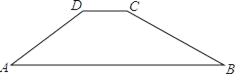
【题目】如图所示,某水库大坝的横断面是梯形ABCD,坝顶宽CD=3m,斜坡AD=8m,斜坡BC的坡度i=1:3,B,C间的水平距离为12m,则斜坡AD的坡角∠A=_____,坝底宽AB=______m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA、PB是⊙O的切线,A、B为切点,∠APB=60°,连接PO并延长与⊙O交于C点,连接AC,BC.
(1)求证:四边形ACBP是菱形;
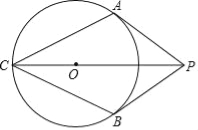
(2)若⊙O半径为1,求菱形ACBP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数图象的顶点坐标是(3,5),且抛物线经过点A(1,3).
(1)求此抛物线的表达式;
(2)如果点A关于该抛物线对称轴的对称点是B点,且抛物线与y轴的交点是C点,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,小明和父母一起开车到距家200千米的景点旅游.出发前,汽车油箱内储油45升;当行驶150千米时,发现油箱剩余油量为30升.
(1)已知油箱内余油量y(升)是行驶路程x(千米)的一次函数,求y与x的函数关系式;
(2)当油箱中余油量少于3升时,汽车将自动报警.如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com