
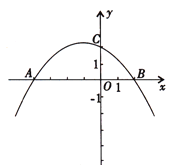
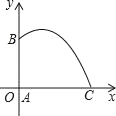
【题目】如图,抛物线![]() (
(![]() ≠0)与
≠0)与![]() 轴交于A(-4,0),B(2,0),与
轴交于A(-4,0),B(2,0),与![]() 轴交与点C(0,2).
轴交与点C(0,2).
(1)求抛物线的解析式;
(2)若点D为该抛物线上的一个动点,且在直线AC上方,当以A,C,D为顶点的三角形面积最大时,求点D的坐标及此时三角形的面积;
【答案】(1)y=﹣![]() x2﹣
x2﹣![]() x+2;(2)S△ADC的最大值为2,此时D(﹣2,2).
x+2;(2)S△ADC的最大值为2,此时D(﹣2,2).
【解析】
(1)根据A与B坐标设出抛物线解析式,将C坐标代入即可求出;
(2)过点D作DH⊥AB于点H,交直线AC于点G,连接DC,AD,如图所示,利用待定系数法求出直线AC解析式,设D横坐标为m,则有G横坐标也为m,表示出DH与GH,由DH-GH表示出DG,三角形ADC面积=三角形ADG面积+三角形DGC面积,表示出面积与m的关系式,利用二次函数性质确定出面积的最大值,以及此时m的值,即此时D的坐标即可.
(1)根据题意设抛物线解析式为y=a(x+4)(x﹣2),
把C(0,2)代入得:﹣8a=2,即a=﹣![]() ,
,
则抛物线解析式为y=﹣![]() (x+4)(x﹣2)=﹣
(x+4)(x﹣2)=﹣![]() x2﹣
x2﹣![]() x+2;
x+2;
(2)过点D作DH⊥AB于点H,交直线AC于点G,连接DC,AD,如图所示,

设直线AC解析式为y=kx+t,则有
![]() ,
,
解得:![]() ,
,
∴直线AC解析式为y=![]() x+2,
x+2,
设点D的横坐标为m,则G横坐标也为m,
∴DH=﹣![]() m2﹣
m2﹣![]() m+2,GH=
m+2,GH=![]() m+2,
m+2,
∴DG=﹣![]() m2﹣
m2﹣![]() m+2﹣
m+2﹣![]() m﹣2=﹣
m﹣2=﹣![]() m2﹣m,
m2﹣m,
∴S△ADC=S△ADG+S△CDG=![]() DGAH+
DGAH+![]() DGOH=
DGOH=![]() DGAO=2DG=﹣
DGAO=2DG=﹣![]() m2﹣2m=﹣
m2﹣2m=﹣![]() (m2+4m)=﹣
(m2+4m)=﹣![]() [(m+2)2﹣4]=﹣
[(m+2)2﹣4]=﹣![]() (m+2)2+2,
(m+2)2+2,
当m=﹣2时,S△ADC取得最大值2,此时yD=﹣![]() ×(﹣2)2﹣
×(﹣2)2﹣![]() ×(﹣2)+2=2,即D(﹣2,2).
×(﹣2)+2=2,即D(﹣2,2).


科目:初中数学 来源: 题型:
【题目】我们知道,在平面内,如果一个图形绕着一个定点旋转一定的角度后能与自身重合,那么就称这个图形是旋转对称图形,转的这个角称为这个图形的一个旋转角.例如,正方形绕着它的对角线的交点旋转![]() 后能与自身重合所以正方形是旋转对称图形,它有一个旋转角为
后能与自身重合所以正方形是旋转对称图形,它有一个旋转角为![]() .
.
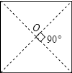
![]() 判断下列说法是否正确(在相应横线里填上“对”或“错”)
判断下列说法是否正确(在相应横线里填上“对”或“错”)
①正五边形是旋转对称图形,它有一个旋转角为![]() .________
.________
②长方形是旋转对称图形,它有一个旋转角为![]() .________
.________
![]() 填空:下列图形中时旋转对称图形,且有一个旋转角为
填空:下列图形中时旋转对称图形,且有一个旋转角为![]() 的是________.(写出所有正确结论的序号)
的是________.(写出所有正确结论的序号)
①正三角形②正方形③正六边形④正八边形
![]() 写出两个多边形,它们都是旋转对称图形,都有一个旋转角为
写出两个多边形,它们都是旋转对称图形,都有一个旋转角为![]() ,其中一个是轴对称图形,但不是中心对称图形;另一个既是轴对称图形,又是中心对称图形.
,其中一个是轴对称图形,但不是中心对称图形;另一个既是轴对称图形,又是中心对称图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:小明同学进入初二以后,读书越发认真.
在学习“用因式分解法解方程”时,课后习题中有这样一个问题:
下列方程的解法对不对?为什么?![]()
解:![]() 或
或![]() .
.
解得![]() 或
或![]() .
.
所以![]() ,
,![]() .
.
同学们都认为不对,原因:有的说该题的因式分解是错误的;有的说将答案代入方程,方程左右两边不成立,等等.
小明同学除了认为该解法不正确,还给出了一种因式分解的做法,小明同学的做法如下:
取![]() 与
与![]() 的平均值
的平均值![]() ,即将
,即将![]() 与
与![]() 相加再除以2.
相加再除以2.
那么原方程可化为![]() .
.
左边用平方差公式可化为![]() .
.
再移项,开平方可得![]()
请你认真阅读小明同学的方法,并用这个方法推导:
关于![]() 的方程
的方程![]() 的求根公式(此时
的求根公式(此时![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:如图1:在四边形ABCD中,AB=AD,∠BAD=120 ,∠B=∠ADC=90°.E、F分别是 BC,CD 上的点。且∠EAF=60° . 探究图中线段BE,EF,FD 之间的数量关系。 小王同学探究此问题的方法是,延长 FD 到点 G,使 DG=BE,连结 AG,先证明△ABE≌△ADG, 再证明△AEF≌△AGF,可得出结论,他的结论应是_________;
探索延伸:如图2,若四边形ABCD中,AB=AD,∠B+∠D=180° .E,F 分别是 BC,CD 上的点,且∠EAF=![]() ∠BAD,上述结论是否仍然成立,并说明理由;
∠BAD,上述结论是否仍然成立,并说明理由;
实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东 70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以55 海里/小时的速度前进,舰艇乙沿北偏东 50°的方向以 75 海里/小时的速度前进2小时后, 指挥中心观测到甲、乙两舰艇分别到达 E,F 处,且两舰艇之间的夹角为70° ,试求此时两舰 艇之间的距离。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解同学们对垃圾分类知识的知晓程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识.某校环保社团的同学们设计了“垃圾分类知识及投放情况”的问卷,并在本校随机抽取了若干名同学进行了问卷测试,根据测试成绩分布情况,他们将全部成绩分成A,B,C,D四组,并绘制了如下不完整的统计图表:
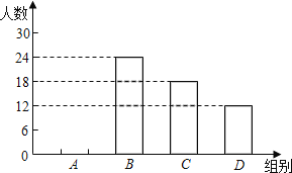
组别 | 分数段 | 频数 | 频率 |
A | 60≤x<70 | a | b |
B | 70≤x<80 | 24 | 0.4 |
C | 80≤x<90 | 18 | c |
D | 90≤x<100 | 12 | 0.2 |
请根据上述统计图表,解答下列问题:
(1)共抽取了多少名学生进行问卷测试?
(2)补全频数分布直方图;
(3)如果测试成绩不低于80分者为“优秀”,请你估计全校2000名学生中,“优秀”等次的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
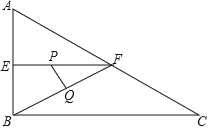
【题目】如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,AB=2cm,E、F分别是AB、AC的中点,动点P从点E出发,沿EF方向匀速运动,速度为1cm/s,同时动点Q从点B出发,沿BF方向匀速运动,速度为2cm/s,连接PQ,设运动时间为ts(0<t<1),则当t=___时,△PQF为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车在某次行驶过程中,油箱中的剩余油量y(升)与行驶路程x(千米)之间是一次函数关系,其部分图象如图所示.
(1)求y关于x的函数关系式;(不需要写定义域)
(2)已知当油箱中的剩余油量为8升时,该汽车会开始提示加油,在此次行驶过程中,行驶了500千米时,司机发现离前方最近的加油站有30千米的路程,在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是多少千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】改革开放后,不少农村用上了自动喷灌设备.如图所示,AB表示水管,在B处有一个自动旋转的喷水头,一瞬间喷出的水是抛物线状,建立如图所示的直角坐标系后,抛物线的表达式为y=﹣![]() x2+2x+
x2+2x+![]() .
.
(1)当x=1时,喷出的水离地面多高?
(2)你能求出水的落地点距水管底部A的最远距离吗?
(3)水管有多高?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com