
如图,正方形ABCD的边长为3,E,F 分别是AB,BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM;
(2)当AE=1时,求EF的长.
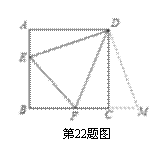
(1)证明:∵ △DAE逆时针旋转90°得到△DCM,∴ ∠FCM=∠FCD+∠DCM=180°,
∴ F,C,M三点共线,DE=DM,∠EDM=90°,∴ ∠EDF+∠FDM=90°.
∵ ∠EDF=45°,∴ ∠FDM=∠EDF=45°.
在△DEF和△DMF中,DE=DM,∠EDF=∠MDF,DF=DF,
∴ △DEF≌△DMF(SAS),∴ EF=MF.
(2)解:设EF=MF=x,∵ AE=CM=1,且BC=3,∴ BM=BC+CM=3+1=4,
∴ BF=BM-MF=BM-EF=4-x.
∵ EB=AB-AE=3-1=2,在Rt△EBF中,
由勾股定理得EB2+BF2=EF2,即22+(4-x)2=x2,
解得:x= ,即EF=
,即EF= .
.


科目:初中数学 来源: 题型:
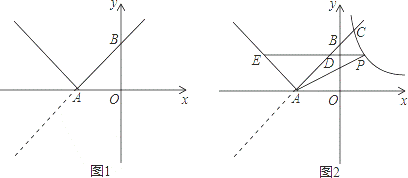
如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,将直线在x轴下方的部分沿x轴翻折,得到一个新函数的图象(图中的“V形折线”).
(1)类比研究函数图象的方法,请列举新函数的两条性质,并求新函数的解析式;
(2)如图2,双曲线y=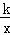 与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.
与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.
①试求△PAD的面积的最大值;
②探索:在点D运动的过程中,四边形PAEC能否为平行四边形?若能,求出此时点D的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,菱形ABCD中,AB=2,∠A=120º,点P、Q、K分别为线段BC、CD、BD上任意一点,则PK+QK的最小值为………………………………………………( )
A.1 B.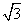 C.2 D.
C.2 D.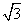 +1
+1
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
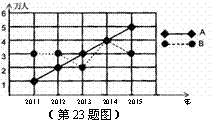
如图所示,A、B两个旅游点从2011年至2015年“清明小长假”期间的旅游人数变化情况分别用实线和虚线表示,请解答以下问题:
(1)B旅游点的旅游人数相对上一年,增长最快的是哪一年?
(2)求A、B两个旅游点从2011年到2015年旅游人数的平均数和方差,并从平均数和方差的角度,用一句话对这两个旅游点的情况进行评价;
(3)A旅游点现在的门票价格为每人80元,为保护旅游点环境和游客的安全,A旅游点的最佳接待人数为4万人. A旅游点决定提高门票价格来控制游客数量. 已知游客数量y(万人)与门票价格x(元)之间满足函数关系y=5-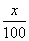 . 若要使A旅游点的游客人数不超过4万人,则门票价格至少应提高多少元?
. 若要使A旅游点的游客人数不超过4万人,则门票价格至少应提高多少元?
 | |||
 | |||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com