Question

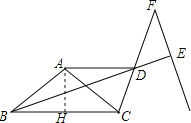
【题目】如本题图①，在△ABC中，已知∠ABC=∠ACB=α．过点A作BC的平行线与∠ABC的平分线交于点D，连接CD．

（1）求∠ACD的大小；

（2）在线段CD的延长线上取一点F，以FD为角的一边作∠DFE=α，另一边交BD延长线于点E，若FD=kAD（如本题图②所示），试求的值（用含k的代数式表示）．

Answer 1

【答案】（1）∠ACD=90°﹣；（2）=k2.

【解析】试题分析：（1）由∠ABC=∠ACB，BD平分∠ABC，得到∠1=∠2=，AB=AC，因为AD∥BC，推出∠2=∠3，得到∠3=∠1=，得到AB=AD．AC=AD=AB．于是得到∠ACD=∠ADC=，根据AD∥BC，∠CAD=ACB=α，得出结论∠ACD=∠ADC==90°﹣．

（2）过A作AH⊥BC于点H，得到∠AHB=90°．证出∠BAH=90°﹣α，因为AD∥BC，得出∠BDC+∠ADC=180°，然后证得对应角相等，得到相似三角形，根据相似三角形的性质得比例式求得结果．

试题解析：（1）∵∠ABC=∠ACB，BD平分∠ABC，∴∠1=∠2=，AB=AC，

∵AD∥BC，∴∠2=∠3，∴∠3=∠1=，∴AB=AD．

∴AC=AD=AB．∴∠ACD=∠ADC=，

又∵AD∥BC，∴∠CAD=ACB=α，

∴∠ACD=∠ADC==90°﹣；

（2）过A作AH⊥BC于点H，则∠AHB=90°．

∴∠BAH=90°﹣α，

∵AD∥BC，∴∠BDC+∠ADC=180°，即：∠BCA+∠ACD+∠CDB+∠3=180°，

由∠ACB=α，∠ACD=90°﹣，∠3=，

得：∠CDB=180°﹣α﹣（90°﹣）﹣=90°﹣α．

∴∠FDE=∠CDB=90°﹣α，∴∠BAH=∠FDE，∵∠ABH=∠DFE=α，

∴△ABH∽△DEF，

∵FD=kAD，AB=AD，∴S△DEF=k2S△BAH，

∵AD∥BC，∴S△BCD=S△ABC=2S△BAH，∴=k2，