
【题目】已知抛物线![]() (a、b、c是常数,
(a、b、c是常数,![]() )的对称轴为直线
)的对称轴为直线![]() .
.
(1) b=______;(用含a的代数式表示)
(2)当![]() 时,若关于x的方程
时,若关于x的方程![]() 在
在![]() 的范围内有解,求c的取值范围;
的范围内有解,求c的取值范围;
(3)若抛物线过点(![]() ,
,![]() ),当
),当![]() 时,抛物线上的点到x轴距离的最大值为4,求a的值.
时,抛物线上的点到x轴距离的最大值为4,求a的值.
【答案】(1)4a;(2)见解析;(3) ![]() 或
或![]() .
.
【解析】分析:(1)由抛物线对称轴方程可以求解;
(2)当a = -1时, 抛物线y= x2 +4x=(x+2)2 -4与直线y = c在-3 <x<1的范围内有交点. 故可得-4≤ c< 5;
(3)由抛物线的对称性结合抛物线上的点到x轴距离的最大值为4可求解.
详解:(1)∵抛物线![]() (a、b、c是常数,
(a、b、c是常数,![]() )的对称轴为直线
)的对称轴为直线![]() ,
,
∴![]() ,
,
∴b=4a ;
(2)当a = -1时,∵关于x的方程![]() 在-3< x <1的范围内有解,即关于x 的方程x2+4x -c=0在-3< x <1的范围内有解,
在-3< x <1的范围内有解,即关于x 的方程x2+4x -c=0在-3< x <1的范围内有解,
∴b2 -4ac =16+4c ≥0,即c ≥ -4.
∴抛物线y= x2 +4x=(x+2)2 -4与直线y = c在-3 <x<1的范围内有交点.
当x= -2时,y= -4,当x=1时,y= 5.
故可得: -4≤ c< 5.
(3)∵抛物线y=ax2+4ax+c过点(-2,-2),
∴c = 4a -2.
∴抛物线解析式为:![]() .
.
① 当a > 0时,抛物线开口向上.
∵抛物线对称轴为x=-2.
∴当-1≤x≤0时,y随x增大而增大.
∵抛物线上的点到x轴距离的最大值为4,
由图像可知:4a -2=4.
∴![]() .
.
② 当a < 0时,抛物线开口向下.
∵抛物线对称轴为x=-2.
∴当-1≤x≤0时,y随x增大而减小.
∵抛物线上的点到x轴距离的最大值为4,
由图像可知:4a -2= -4.
∴![]() .
.
综上所述: ![]() .
.


科目:初中数学 来源: 题型:
【题目】计算
(1) -20+(-18)-12 +10
(2)![]()
(3) ![]()
(4)(-81)÷2![]() ×(-
×(-![]() )÷(-16)
)÷(-16)
(5) (-36) ÷4-5×(-1.2)
(6)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,点E,F分别在边AD、BC上,EF=2,∠DEF=60°将四边形EFCD沿EF翻折,得到四边形EFC’D’,ED’交BC于点G,则△GEF的周长为________.
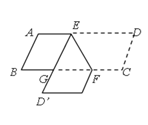
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则B5的坐标是_____________ 。
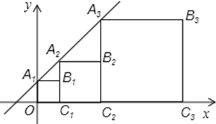
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:我们知道:如果点A.B在数轴上分别表示有理数a、b,那么A.B两点之间的距离表示为AB,在数轴上A.B两点之间的距离AB=|ab|.
根据上述材料,利用数轴解答下列问题:
![]()
(1)如果点A在数轴上表示2,将点A先向左平移2个单位长度,再向右移动7个单位长度,那么终点B在数轴上表示的数是___;
(2)数轴上表示x和1的两个点之间的距离是___;
(3)若|x3|+|x+2|=7,则x的值是___;
(4)在(1)的条件下,设点P在数轴上表示的数为x,当|PA||PB|=2时,则x的值是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为2,
的边长为2, ![]() 边在
边在![]() 轴上,
轴上, ![]() 的中点与原点
的中点与原点![]() 重合,过定点
重合,过定点![]() 与动点
与动点![]() 的直线
的直线![]() 记作
记作![]() .
.

(1)若![]() 的解析式为
的解析式为![]() ,判断此时点
,判断此时点![]() 是否在直线
是否在直线![]() 上,并说明理由;
上,并说明理由;
(2)当直线![]() 与
与![]() 边有公共点时,求
边有公共点时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】聪聪参加我市电视台组织的“阳光杯”智力竞答节目,答对最后两道单选题就顺利通关,第一道单选题有![]() 个选项,第二道单选题有4个选项,这两道题聪聪都不会,不过聪聪还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
个选项,第二道单选题有4个选项,这两道题聪聪都不会,不过聪聪还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
(1)如果聪聪两次“求助”都在第一道题中使用,那么聪聪通关的概率是 .
(2)如果聪聪将每道题各用一次“求助”,请用树状图或者列表来分析他顺利通关的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com