
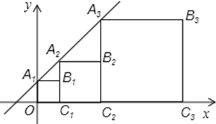
【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则B5的坐标是_____________ 。
【答案】(31,16)
【解析】
首先由B1的坐标为(1,1),点B2的坐标为(3,2),可得正方形A1B1C1O1边长为1,正方形A2B2C2C1边长为2,即可求得A1的坐标是(0,1),A2的坐标是:(1,2),然后又待定系数法求得直线A1A2的解析式,由解析式即可求得点A3的坐标,继而可得点B3的坐标,观察可得规律Bn的坐标是(2n-1,2n-1).
∵B1的坐标为(1,1),点B2的坐标为(3,2)
∴正方形A1B1C1O1边长为1,正方形A2B2C2C1边长为2
∴A1的坐标是(0,1),A2的坐标是:(1,2)
设直线A1A2的解析式为:y=kx+b
∴![]()
解得:![]()
∴直线A1A2的解析式是:y=x+1
∵点B2的坐标为(3,2)
∴点A3的坐标为(3,4)
∴点B3的坐标为(7,4)
∴Bn的横坐标是:2n-1,纵坐标是:2n1
∴Bn的坐标是(2n1,2n1)
故点B5的坐标为(31,16).


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】为弘扬中华优秀传统文化,某校开展“经典诵读”比赛活动,诵读材料有《论语》、《大学》、《中庸》(依次用字母A,B,C表示这三个材料),将A,B,C分别写在3张完全相同的不透明卡片的正面上,背面朝上洗匀后放在桌面上,比赛时小礼先从中随机抽取一张卡片,记下内容后放回,洗匀后,再由小智从中随机抽取一张卡片,他俩按各自抽取的内容进行诵读比赛.
(1)小礼诵读《论语》的概率是 ;(直接写出答案)
(2)请用列表或画树状图的方法求他俩诵读两个不同材料的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时![]() 张用A方法,其余用B方法。
张用A方法,其余用B方法。
(1)用![]() 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
科目:初中数学 来源: 题型:
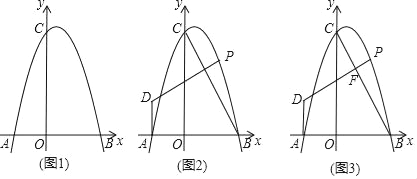
【题目】已知:如图,抛物线y=ax2+bx+6交x轴于A(﹣2,0),B(3,0)两点,交y轴于点C.
(1)求a,b的值;
(2)连接BC,点P为第一象限抛物线上一点,过点A作AD⊥x轴,过点P作PD⊥BC于交直线AD于点D,设点P的横坐标为t,AD长为d,求d与t的函数关系式(请求出自变量t的取值范围);
(3)在(2)的条件下,DP与BC交于点F,过点D作DE∥AB交BC于点E,点Q为直线DP上方抛物线上一点,连接AP、PC,若DP=CE,∠QPC=∠APD时,求点Q坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
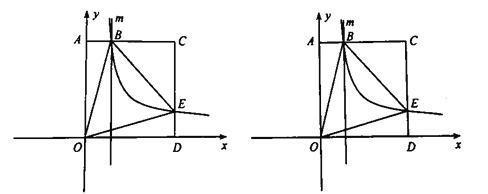
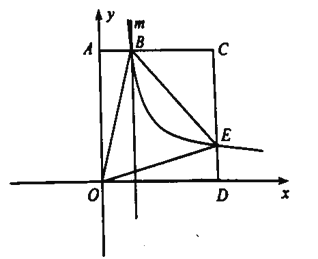
【题目】如图,边长为3正方形![]() 的顶点
的顶点![]() 与原点重合,点
与原点重合,点![]() 在
在![]() 轴,
轴,![]() 轴上。反比例函数
轴上。反比例函数![]() 的图象交
的图象交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)求反比例函数的解析式;
(2)过点![]() 作
作![]() 轴的平行线
轴的平行线![]() ,点
,点![]() 在直线
在直线![]() 上运动,点
上运动,点![]() 在
在![]() 轴上运动.
轴上运动.
①若![]() 是以
是以![]() 为直角顶点的等腰直角三角形,求
为直角顶点的等腰直角三角形,求![]() 的面积;
的面积;
②将“①”中的“以![]() 为直角顶点的”去掉,将问题改为“若
为直角顶点的”去掉,将问题改为“若![]() 是等腰直角三角形”,
是等腰直角三角形”,![]() 的面积除了“①”中求得的结果外,还可以是______.(直接写答案,不用写步骤)
的面积除了“①”中求得的结果外,还可以是______.(直接写答案,不用写步骤)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠B=54°,AD是△ABC的角平分线.求作AB的垂直平分线MN交AD于点E,连接BE;并证明DE=DB.(要求:尺规作图,保留作图痕迹,不写作法)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (a、b、c是常数,
(a、b、c是常数,![]() )的对称轴为直线
)的对称轴为直线![]() .
.
(1) b=______;(用含a的代数式表示)
(2)当![]() 时,若关于x的方程
时,若关于x的方程![]() 在
在![]() 的范围内有解,求c的取值范围;
的范围内有解,求c的取值范围;
(3)若抛物线过点(![]() ,
,![]() ),当
),当![]() 时,抛物线上的点到x轴距离的最大值为4,求a的值.
时,抛物线上的点到x轴距离的最大值为4,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以坐标原点O为圆心,2为半径画圆,P是⊙O上一动点且在第一象限内,过点P作⊙O的切线,与x、y轴分别交于点A、B.
(1)求证:△OBP与△OPA相似;
(2)当点P为AB中点时,求出P点坐标;
(3)在⊙O上是否存在一点Q,使得以Q,O,A、P为顶点的四边形是平行四边形.若存在,试求出Q点坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com