
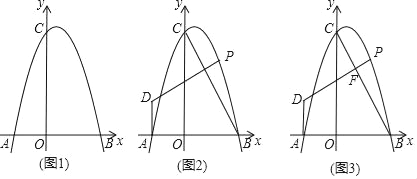
【题目】已知:如图,抛物线y=ax2+bx+6交x轴于A(﹣2,0),B(3,0)两点,交y轴于点C.
(1)求a,b的值;
(2)连接BC,点P为第一象限抛物线上一点,过点A作AD⊥x轴,过点P作PD⊥BC于交直线AD于点D,设点P的横坐标为t,AD长为d,求d与t的函数关系式(请求出自变量t的取值范围);
(3)在(2)的条件下,DP与BC交于点F,过点D作DE∥AB交BC于点E,点Q为直线DP上方抛物线上一点,连接AP、PC,若DP=CE,∠QPC=∠APD时,求点Q坐标.
【答案】(1)a=-1,b=1;(2)d=﹣t2+![]() t+5(0<t<3);(3)点Q坐标为Q(1,6)或Q(﹣
t+5(0<t<3);(3)点Q坐标为Q(1,6)或Q(﹣![]() ,
, ![]() ).
).
【解析】试题分析:
(1)把A、B两点的坐标代入抛物线的解析式列出关于a、b的二元一次方程组,解方程组即可求得a、b的值;
(2)如下图2、过点P作PG⊥DE于点K,交x轴于点G,作DK⊥PG于点K,则由已知条件易得∠BCO=∠PDK,由此可得tan∠PDK=![]() =tan∠BCO,结合OB=3,OC=6,DK=t+2可得PK=
=tan∠BCO,结合OB=3,OC=6,DK=t+2可得PK=![]() DK=
DK=![]() (t+2);再证四边形ADKG是矩形可得KG=AD=d=PG-PK结合PG=-t2+t+6即可得到d与t间的函数关系式了,由点P在第一象限的图象上可得0<t<3;
(t+2);再证四边形ADKG是矩形可得KG=AD=d=PG-PK结合PG=-t2+t+6即可得到d与t间的函数关系式了,由点P在第一象限的图象上可得0<t<3;
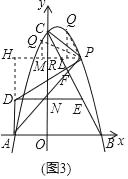
(3)如下图3,过点P作PH⊥AD于点H交y轴于点R,由已知条件易证△PHD≌△CNE,从而可得PH=CN,结合CN=OC-ON,PH=t+2可得关于t的方程t+2=t2﹣![]() t+1,解方程可得t1=2,t2=﹣
t+1,解方程可得t1=2,t2=﹣![]() (舍),把t=2代入抛物线y=﹣x2+x+6=4,可得点P(2,4),由此可得PR=CR,PH=AH,从而可得∠APC=90°结合∠QPC=∠APD可得∠QPD=90°,然后分点P在第一象限的抛物线上和第三象限的抛物线上两种情况讨论计算即可得到对应的点Q的坐标.
(舍),把t=2代入抛物线y=﹣x2+x+6=4,可得点P(2,4),由此可得PR=CR,PH=AH,从而可得∠APC=90°结合∠QPC=∠APD可得∠QPD=90°,然后分点P在第一象限的抛物线上和第三象限的抛物线上两种情况讨论计算即可得到对应的点Q的坐标.
试题解析:
(1)∵抛物线y=ax2+bx+6过点A(﹣2,0),B(3,0),则
![]() ,解得:
,解得: ![]() ,
,
故抛物线解析式为y=﹣x2+x+6;
(2)如下图2,过点P作PG⊥x于点G,过点D作DK∥x轴交PG于点K,
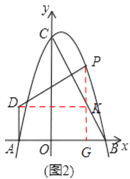
∵PD⊥BC,DE⊥y轴,∠BCO=∠PDK,OB=3,OC=6
∴tan∠BCO=tan∠PDK=![]() ,DK=t+2,PK=
,DK=t+2,PK=![]() DK=
DK=![]() (t+2),
(t+2),
∵DK∥AB,AD⊥AB,
∴四边形ADKG为矩形,
∴AD=KG,
d=AD=KG=PG﹣PK=﹣t2+t+6﹣![]() (t+2)=﹣t2+
(t+2)=﹣t2+![]() t+5(0<t<3);
t+5(0<t<3);
(3)如图3,过点P作PH⊥AD于点H,
在△PHD与△CNE中, 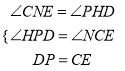 ,
,
∴△PHD≌△CNE,
∴PH=CN=OC﹣ON,
∵四边形ADON为矩形,
∴CN=6﹣(﹣t2+![]() t+5)=t2﹣
t+5)=t2﹣![]() t+1,PH=t+2,
t+1,PH=t+2,
∴t+2=t2﹣![]() t+1,
t+1,
解得t1=2,t2=﹣![]() (舍),
(舍),
把t=2代入抛物线y=﹣x2+x+6=4,
∴点P(2,4),
∵PH与y轴交于点R,PR=CR=2,
∴∠CPR=45°,PH=AH=4,
∴∠APH=45°,
∴∠APC=90°,
∵∠QPC=∠APD,
∴∠QPD=90°,
当点Q在第一象限时,过点Q作QL⊥PH于点L,
∴∠LQP=∠HPD,
∴tan∠LQP=tan∠HPD=![]() ,
,
设点Q(m,﹣m2+m+6),则PL=2﹣m,QL=﹣m2+m+2,则
![]() =
=![]() ,
,
解得m1=1,m2=2(舍),
把m=1 代入﹣m2+m+6=6,
∴Q(1,6),
当点Q在第二象限时,过点Q作QM⊥PH,
∵∠CPH=∠APH=45°∠QPC=∠APD,
∴∠QPM=∠DPH tan∠QPM=tan∠DPH=![]() ,
,
设点Q(n,﹣n2+n+6)PM=2﹣n QM=﹣n2+n+2,
∴![]() =
=![]() ,
,
解得n1=﹣![]() ,n2=2(舍),
,n2=2(舍),
把n=1﹣![]() 代入﹣n2+n+6=
代入﹣n2+n+6=![]() ,
,
∴Q(﹣![]() ,
, ![]() ).
).
综上所述,点Q坐标为Q(1,6)或Q(﹣![]() ,
, ![]() ).
).


科目:初中数学 来源: 题型:
【题目】某个“清凉小屋”自动售货机出售![]() 三种饮料.
三种饮料.![]() 三种饮料的单价分别是2元/瓶、3元/瓶、5元/瓶. 工作日期间,每天上货量是固定的,且能全部售出,其中,
三种饮料的单价分别是2元/瓶、3元/瓶、5元/瓶. 工作日期间,每天上货量是固定的,且能全部售出,其中,![]() 饮料的数量(单位:瓶)是
饮料的数量(单位:瓶)是![]() 饮料数量的2倍,
饮料数量的2倍,![]() 饮料的数量(单位:瓶)是
饮料的数量(单位:瓶)是![]() 饮料数量的2倍. 某个周六,
饮料数量的2倍. 某个周六,![]() 三种饮料的上货量分别比一个工作日的上货量增加了50%,60%,50%,且全部售出. 但是由于软件bug,发生了一起错单(即消费者按某种饮料1瓶的价格投币,但是取得了另一种饮料1瓶),结果这个周六的销售收入比一个工作日的销售收入多了403元. 则这个“清凉小屋”自动售货机一个工作日的销售收入是__________元.
三种饮料的上货量分别比一个工作日的上货量增加了50%,60%,50%,且全部售出. 但是由于软件bug,发生了一起错单(即消费者按某种饮料1瓶的价格投币,但是取得了另一种饮料1瓶),结果这个周六的销售收入比一个工作日的销售收入多了403元. 则这个“清凉小屋”自动售货机一个工作日的销售收入是__________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
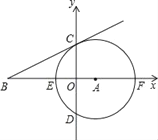
【题目】在直角坐标系中,⊙A的半径为4,圆心A的坐标为(2,0),与x轴交于E、F两点,与y轴交于C、D两点,过点C作⊙A的切线BC,交x轴于B.
(1)求直线CB的解析式;
(2)若抛物线y=ax2+bx+c的顶点在直线BC上,与x轴交的点恰为⊙A与x轴的交点,求该抛物线的解析式;
(3)试判断C是否在抛物线上?
查看答案和解析>>
科目:初中数学 来源: 题型:
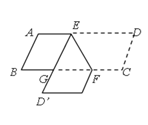
【题目】如图,在□ABCD中,点E,F分别在边AD、BC上,EF=2,∠DEF=60°将四边形EFCD沿EF翻折,得到四边形EFC’D’,ED’交BC于点G,则△GEF的周长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
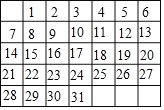
【题目】如图是某月的月历,用一个矩形框,每次框住9个数.若这9个数之和是81,则这9个数中最大的数为_____,这9个数之和可能会是100吗?_____(填“能”或“不能”)
查看答案和解析>>
科目:初中数学 来源: 题型:
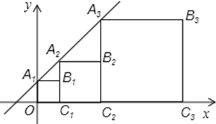
【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则B5的坐标是_____________ 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区教育局为了解今年九年级学生体育测试情况,随机抽查了某班学生的体育测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题:


说明:A级:90分~100分;B级:75分~89分;C级:60分~74分;D级:60分以下
(1)样本中D级的学生人数占全班学生人数的百分比是 ;
(2)扇形统计图中A级所在的扇形的圆心角度数是 ;
(3)请把条形统计图补充完整;
(4)若该校九年级有500名学生,请你用此样本估计体育测试中A级和B级的学生人数之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com