
【题目】解方程
(1)6﹣4(x+2)=3(x﹣3)
(2)![]() ﹣1
﹣1
(3)![]() =1
=1
(4)![]()
【答案】(1)x=1;(2)x=![]() ;(3)x=
;(3)x=![]() ;(4)x=
;(4)x=![]() .
.
【解析】
(1)方程去括号,移项,合并同类项,把x系数化为1,即可求出解;
(2)方程去分母,去括号,移项,合并同类项,把x系数化为1,即可求出解;
(3)方程整理后,去分母,去括号,移项,合并同类项,把x系数化为1,即可求出解;
(4)方程整理后,移项,合并同类项,把x系数化为1,即可求出解.
解:(1)去括号得:6﹣4x﹣8=3x﹣9,
移项得:﹣4x﹣3x=﹣9+8-6,
合并同类项得:﹣7x=﹣7,
解得:x=1;
(2)去分母得:8x﹣4﹣20x+2=6x+3﹣12,
移项得:8x﹣6x﹣20x=3﹣12+4-2,
合并同类项得:﹣18x=﹣7,
解得:x=![]() ;
;
(3)方程整理得:![]() ,
,
去分母得:9x+60﹣20x﹣8=6,
移项得:9x﹣20x=6-60+8,
合并同类项得:﹣11x=﹣46,
解得:x=![]() ;
;
(4)方程整理得:![]() ,
,
移项得:![]() ,
,
合并同类项得:![]() ,
,
解得:x=![]() .
.


科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,某市自来水公司对每户用水量进行了分段计费,每户每月用水量在规定吨数以下的收费标准相同,规定吨数以上的超过部分收费相同.如表是小明家1﹣4月用水量和交费情况:
月份 | 1 | 2 | 3 | 4 |
用水量(吨) | 6 | 8 | 12 | 15 |
费用(元) | 12 | 16 | 28 | 37 |
(Ⅰ)若小明家5月份用水25吨,则应缴多少元水费?
(Ⅱ)若该户居民某月份用水为![]() 吨,则应收水费多少元?(用含
吨,则应收水费多少元?(用含![]() 的代数式表示,并化简).
的代数式表示,并化简).
查看答案和解析>>
科目:初中数学 来源: 题型:
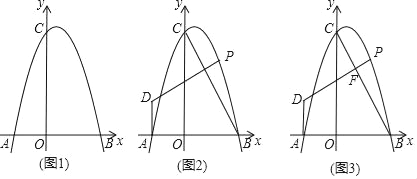
【题目】已知:如图,抛物线y=ax2+bx+6交x轴于A(﹣2,0),B(3,0)两点,交y轴于点C.
(1)求a,b的值;
(2)连接BC,点P为第一象限抛物线上一点,过点A作AD⊥x轴,过点P作PD⊥BC于交直线AD于点D,设点P的横坐标为t,AD长为d,求d与t的函数关系式(请求出自变量t的取值范围);
(3)在(2)的条件下,DP与BC交于点F,过点D作DE∥AB交BC于点E,点Q为直线DP上方抛物线上一点,连接AP、PC,若DP=CE,∠QPC=∠APD时,求点Q坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠B=54°,AD是△ABC的角平分线.求作AB的垂直平分线MN交AD于点E,连接BE;并证明DE=DB.(要求:尺规作图,保留作图痕迹,不写作法)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (a、b、c是常数,
(a、b、c是常数,![]() )的对称轴为直线
)的对称轴为直线![]() .
.
(1) b=______;(用含a的代数式表示)
(2)当![]() 时,若关于x的方程
时,若关于x的方程![]() 在
在![]() 的范围内有解,求c的取值范围;
的范围内有解,求c的取值范围;
(3)若抛物线过点(![]() ,
,![]() ),当
),当![]() 时,抛物线上的点到x轴距离的最大值为4,求a的值.
时,抛物线上的点到x轴距离的最大值为4,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
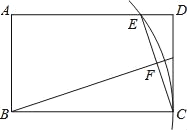
【题目】如图,在矩形ABCD中,AB=3,BC=5,以B为圆心BC为半径画弧交AD于点E,连接CE,作BF⊥CE,垂足为F,则tan∠FBC的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以坐标原点O为圆心,2为半径画圆,P是⊙O上一动点且在第一象限内,过点P作⊙O的切线,与x、y轴分别交于点A、B.
(1)求证:△OBP与△OPA相似;
(2)当点P为AB中点时,求出P点坐标;
(3)在⊙O上是否存在一点Q,使得以Q,O,A、P为顶点的四边形是平行四边形.若存在,试求出Q点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知方程组![]() 的解满足x为非正数,y为负数.
的解满足x为非正数,y为负数.
(1)求m的取值范围;
(2)化简:|m﹣3|﹣|m+2|;
(3)在m的取值范围内,当m为何整数时,不等式2mx+x<2m+1的解为x>1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2018年某明星演唱会”于6月3日在某市奥体中心举办.小明去离家300的奥体中心看演唱会,到奥体中心后,发现演唱会门票忘带了,此时离演唱会开始还有30分钟,于是他跑步回家,拿到票后立刻找到一辆“共享单车”原路赶回奥体中心,已知小明骑车的时间比跑步的时间少用了5分钟,且骑车的平均速度是跑步的平均速度的1.5倍.
(1)求小明跑步的平均速度;
(2)如果小明在家取票和寻找“共享单车”共用了4分钟,他能否在演唱会开始前赶到奥体中心?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com