练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

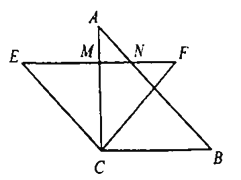
    【题目】把两个全等的等腰直角三角形如图放置在一起，点关于对称交，于点，则与的面积比为（ ）

    A.B.C.D.

    【答案】D

    【解析】

    由轴对称性质得EF⊥AC，由∠A=45°，得出△AMN是等腰直角三角形，由等腰直角三角形的性质得CM=EM=CE，由△ECF≌△ACB得出AC=CE=BC，则AM=（1-）AC，由等腰直角三角形面积公式即可得出结果．

    解：∵△ACB是等腰直角三角形，
    ∴AC=BC，∠A=45°，
    ∵点E，F关于AC对称，
    ∴EF⊥AC，
    ∵∠A=45°，
    ∴△AMN是等腰直角三角形，
    ∵△ECF是等腰直角三角形，
    ∴CM=EM==CE,

    ∵△ECF≌△ACB，
    ∴AC=CE=BC，
    ∴AM=AC-CM=AC-AC=（1-）AC，

    ∴=== = .

    故选：D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下列函数关系中，可以看做二次函数y=a+bx+c模型的是（　　）

    A. 在一定距离内，汽车行驶的速度与行驶的时间的关系

    B. 我国人中自然增长率为1%，这样我国总人口数随年份变化的关系

    C. 竖直向上发射的信号弹，从发射到落回地面，信号弹的高度与时间的关系（不计空气阻力）

    D. 圆的周长与半径之间的关系

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了鼓励市民节约用水，某市自来水公司对每户用水量进行了分段计费，每户每月用水量在规定吨数以下的收费标准相同，规定吨数以上的超过部分收费相同．如表是小明家1﹣4月用水量和交费情况：

    月份

    1

    2

    3

    4

    用水量（吨）

    6

    8

    12

    15

    费用（元）

    12

    16

    28

    37

    （Ⅰ）若小明家5月份用水25吨，则应缴多少元水费？

    （Ⅱ）若该户居民某月份用水为吨，则应收水费多少元？（用含的代数式表示，并化简）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中，，的垂直平分线交于点，交于点，连接，，，，添加一个条件，无法判定四边形为正方形的是（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】用正方形硬纸板做三棱柱盒子，每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪（裁剪后边角料不再利用）

    A方法：剪6个侧面； B方法：剪4个侧面和5个底面。

    现有19张硬纸板，裁剪时张用A方法，其余用B方法。

    （1）用的代数式分别表示裁剪出的侧面和底面的个数；

    （2）若裁剪出的侧面和底面恰好全部用完，问能做多少个盒子？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知多项式2x3y﹣xy+16的次数为a，常数项为b，a，b分别对应着数轴上的A、B两点．

    （1）a＝　 　，b＝　 　；并在数轴上画出A、B两点；

    （2）若点P从点A出发，以每秒3个单位长度单位的速度向x轴正半轴运动，求运动时间为多少时，点P到点A的距离是点P到点B的距离的2倍；

    （3）数轴上还有一点C的坐标为30，若点P和Q同时从点A和点B出发，分别以每秒3个单位长度和每秒1个单位长度的速度向C点运动，P到达C点后，再立即以同样的速度返回，运动的终点A，求点P和点Q运动多少秒时，P，Q两点之间的距离为4，并求出此时点Q的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

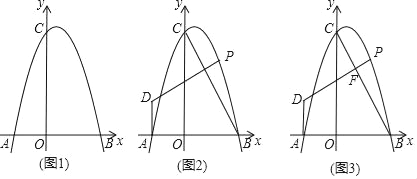
    【题目】已知：如图，抛物线y=ax2+bx+6交x轴于A（﹣2，0），B（3，0）两点，交y轴于点C.

    （1）求a，b的值；

    （2）连接BC，点P为第一象限抛物线上一点，过点A作AD⊥x轴，过点P作PD⊥BC于交直线AD于点D，设点P的横坐标为t，AD长为d，求d与t的函数关系式（请求出自变量t的取值范围）；

    （3）在（2）的条件下，DP与BC交于点F，过点D作DE∥AB交BC于点E，点Q为直线DP上方抛物线上一点，连接AP、PC，若DP=CE，∠QPC=∠APD时，求点Q坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠C＝90°，∠B＝54°，AD是△ABC的角平分线．求作AB的垂直平分线MN交AD于点E，连接BE；并证明DE＝DB．（要求：尺规作图，保留作图痕迹，不写作法）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知方程组的解满足x为非正数，y为负数．

    (1)求m的取值范围；

    (2)化简：|m﹣3|﹣|m+2|；

    (3)在m的取值范围内，当m为何整数时，不等式2mx+x＜2m+1的解为x＞1．

    查看答案和解析>>

    同步练习册答案