
ЁОЬтФПЁПвбжЊЖрЯюЪН2x3yЉxy+16ЕФДЮЪ§ЮЊaЃЌГЃЪ§ЯюЮЊbЃЌaЃЌbЗжБ№ЖдгІзХЪ§жсЩЯЕФAЁЂBСНЕуЃЎ
ЃЈ1ЃЉaЃНЁЁ ЁЁЃЌbЃНЁЁ ЁЁЃЛВЂдкЪ§жсЩЯЛГіAЁЂBСНЕуЃЛ
ЃЈ2ЃЉШєЕуPДгЕуAГіЗЂЃЌвдУПУы3ИіЕЅЮЛГЄЖШЕЅЮЛЕФЫйЖШЯђxжсе§АыжсдЫЖЏЃЌЧѓдЫЖЏЪБМфЮЊЖрЩйЪБЃЌЕуPЕНЕуAЕФОрРыЪЧЕуPЕНЕуBЕФОрРыЕФ2БЖЃЛ
ЃЈ3ЃЉЪ§жсЩЯЛЙгавЛЕуCЕФзјБъЮЊ30ЃЌШєЕуPКЭQЭЌЪБДгЕуAКЭЕуBГіЗЂЃЌЗжБ№вдУПУы3ИіЕЅЮЛГЄЖШКЭУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђCЕудЫЖЏЃЌPЕНДяCЕуКѓЃЌдйСЂМДвдЭЌбљЕФЫйЖШЗЕЛиЃЌдЫЖЏЕФжеЕуAЃЌЧѓЕуPКЭЕуQдЫЖЏЖрЩйУыЪБЃЌPЃЌQСНЕужЎМфЕФОрРыЮЊ4ЃЌВЂЧѓГіДЫЪБЕуQЕФзјБъЃЎ

ЁОД№АИЁПЃЈ1ЃЉ4ЃЌ16ЃЛЭМЯъМћНтЮіЃЛЃЈ2ЃЉtЃН![]() Лђ8ЃЛЃЈ3ЃЉЕуPКЭЕуQдЫЖЏ4Лђ8Лђ9Лђ11УыЪБЃЌPЃЌQСНЕужЎМфЕФОрРыЮЊ4ЃЌЕуQБэЪОЕФЪ§ЮЊ20ЃЌ24ЃЌ25ЃЌ27ЃЎ
Лђ8ЃЛЃЈ3ЃЉЕуPКЭЕуQдЫЖЏ4Лђ8Лђ9Лђ11УыЪБЃЌPЃЌQСНЕужЎМфЕФОрРыЮЊ4ЃЌЕуQБэЪОЕФЪ§ЮЊ20ЃЌ24ЃЌ25ЃЌ27ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЧѓГіaЁЂbЕФжЕМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉЙЙНЈЗНГЬМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉЗжЫФжжЧщаЮЙЙНЈЗНГЬМДПЩНтОіЮЪЬт.
ЃЈ1ЃЉЁпЖрЯюЪН2x3yЉxy+16ЕФДЮЪ§ЮЊaЃЌГЃЪ§ЯюЮЊbЃЌ
ЁрaЃН4ЃЌbЃН16ЃЌ
ЙЪД№АИЮЊ4ЃЌ16ЃЎ
ЕуAЁЂBЕФЮЛжУШчЭМЫљЪОЃЎ

ЃЈ2ЃЉЩшдЫЖЏЪБМфЮЊtsЃЎ
гЩЬтвтЃК3tЃН2ЃЈ16Љ4Љ3tЃЉЛђ3tЃН2ЃЈ4+3tЉ16ЃЉЃЌ
НтЕУtЃН![]() Лђ8ЃЌ
Лђ8ЃЌ
ЁрдЫЖЏЪБМфЮЊ![]() Лђ8УыЪБЃЌЕуPЕНЕуAЕФОрРыЪЧЕуPЕНЕуBЕФОрРыЕФ2БЖЃЛ
Лђ8УыЪБЃЌЕуPЕНЕуAЕФОрРыЪЧЕуPЕНЕуBЕФОрРыЕФ2БЖЃЛ
ЃЈ3ЃЉЩшдЫЖЏЪБМфЮЊtsЃЎЕуPдкдЫЖЏПЊЪМЕННсЪјЙ§ГЬжаДцдкШчЯТЗћКЯЬтвтЕФЫФжжЧщПіЃК
ЕБЕуPдкAЁЂBжЎМфЪБЃЌга3t+4=(16-4)+tЃЌНтЕУt=4, ДЫЪБЕуQБэЪОЕФЪ§ЮЊ20ЃЛ
ЕБЕуPдкBЁЂCжЎМфЪБЃЌга3t-[(16-4) +t]=tЃЌНтЕУt=8, ДЫЪБЕуQБэЪОЕФЪ§ЮЊ24ЃЛ
ЕБPЕНДяЕуCДІКѓЗЕЛиЧвQдкPЕФгвВрЪБЃЌга12+t+4+3tЃН52ЃЌНтЕУt=9,ДЫЪБЕуQБэЪОЕФЪ§ЮЊ25ЃЛ
ЕБPЕНДяжеЕуAЃЌQМЬајдЫЖЏЕНЕуCДІКѓЗЕЛиЃЌВЂгыPЯрОр6ЪБЃЌга12+t+3tЉ4ЃН52ЃЌНтЕУt=11,ДЫЪБЕуQБэЪОЕФЪ§ЮЊ25ЃЎ
ЁрЕуPКЭЕуQдЫЖЏ4Лђ8Лђ9Лђ11УыЪБЃЌPЃЌQСНЕужЎМфЕФОрРыЮЊ4ЃЎ
ДЫЪБЕуQБэЪОЕФЪ§ЮЊ20ЃЌ24ЃЌ25ЃЌ27ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
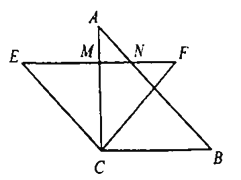
ЁОЬтФПЁПШчЭМЃЌМзЁЂввСНДЌЭЌЪБДгAИлПкГіЗЂЃЌМзДЌвдУПаЁЪБ30КЃРяЕФЫйЖШЯђЮїЦЋББ32ЁуЕФЗНЯђКНаа2аЁЪБЕНДяCЕКЃЌввДЌвдУПаЁЪБ40КЃРяЕФЫйЖШКНаа2аЁЪБЕНBЕКЃЌвбжЊBЁЂCСНЕКЯрОр100КЃРяЃЌЧѓввДЌКНааЕФЗНЯђЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕжаЕФУПИіаЁе§ЗНаЮБпГЄЮЊ1ЃЌЁїABCЕФЖЅЕудкЭјИёЕФИёЕуЩЯЃЎ
ЃЈ1ЃЉЛЯпЖЮADЁЮBCЃЌЧвЪЙADЃНBCЃЌСЌНгBDЃЛДЫЪБDЕуЕФзјБъЪЧЁЁ ЁЁЃЎ
ЃЈ2ЃЉжБНгаДГіЯпЖЮACЕФГЄЮЊЁЁ ЁЁЃЌADЕФГЄЮЊЁЁ ЁЁЃЌBDЕФГЄЮЊЁЁ ЁЁЃЎ
ЃЈ3ЃЉжБНгаДГіЁїABDЮЊЁЁ ЁЁШ§НЧаЮЃЌЫФБпаЮADBCУцЛ§ЪЧЁЁ ЁЁЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃдквЛДЮЯзАЎаФОшПюЛюЖЏжаЃЌбЇаЃЭХжЇВПЮЊСЫНтБОаЃбЇЩњЕФИїРрОшПюШЫЪ§ЕФЧщПіЃЌНјааСЫвЛДЮЭГМЦЕїВщЃЌВЂЛцжЦГЩСЫЭГМЦЭМЂйКЭЂкЃЌЧыНтД№ЯТСаЮЪЬтЃЎ
ЃЈ1ЃЉБОДЮЙВЕїВщСЫЖрЩйУћбЇЩњЃЎ
ЃЈ2ЃЉВЙШЋЬѕаЮЭГМЦЭМЃЎ
ЃЈ3ЃЉетаЉбЇЩњОшПюЪ§ЕФжкЪ§ЮЊЁЁ ЃЌжаЮЛЪ§ЮЊЁЁ ЃЎ
ЃЈ4ЃЉЧѓЦНОљУПИібЇЩњОшПюЖрЩйдЊЃЎ
ЃЈ5ЃЉШєИУаЃга600УћбЇЩњЃЌФЧУДЙВОшПюЖрЩйдЊЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПАбСНИіШЋЕШЕФЕШбќжБНЧШ§НЧаЮШчЭМЗХжУдквЛЦ№![]() ЃЌЕу
ЃЌЕу![]() Йигк
Йигк![]() ЖдГЦ
ЖдГЦ![]() НЛ
НЛ![]() ЃЌ
ЃЌ![]() гкЕу
гкЕу![]() ЃЌдђ
ЃЌдђ![]() гы
гы![]() ЕФУцЛ§БШЮЊЃЈ ЃЉ
ЕФУцЛ§БШЮЊЃЈ ЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌЙ§Еу
ЕФжаЕуЃЌЙ§Еу![]() зї
зї![]() НЛ
НЛ![]() ЕФбгГЄЯпгкЕу
ЕФбгГЄЯпгкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() .
.

ЃЈ1ЃЉаДГіЫФБпаЮ![]() ЕФаЮзДЃЌВЂжЄУїЃК
ЕФаЮзДЃЌВЂжЄУїЃК
ЃЈ2ЃЉШєЫФБпаЮ![]() ЕФУцЛ§ЮЊ12ЃЌ
ЕФУцЛ§ЮЊ12ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧФГдТЕФдТРњЃЌгУвЛИіОиаЮПђЃЌУПДЮПђзЁ9ИіЪ§ЃЎШєет9ИіЪ§жЎКЭЪЧ81ЃЌдђет9ИіЪ§жазюДѓЕФЪ§ЮЊ_____ЃЌет9ИіЪ§жЎКЭПЩФмЛсЪЧ100Т№ЃП_____ЃЈЬюЁАФмЁБЛђЁАВЛФмЁБЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЃКЫљЮНЙДЙЩЪ§ОЭЪЧТњзуЗНГЬx2+y2=z2ЕФе§ећЪ§НтЃЌМДТњзуЙДЙЩЖЈРэЕФШ§Иіе§ећЪ§ЙЙГЩЕФвЛзщЪ§ЃЎЮвЙњЙХДњЪ§бЇзЈжјЁЖОХеТЫуЪѕЁЗвЛЪщЃЌдкЪРНчЩЯЕквЛДЮИјГіИУЗНГЬЕФНтЮЊЃК![]() ЃЌy=mnЃЌ
ЃЌy=mnЃЌ![]() ЃЌЦфжаm>n>0ЃЌmЁЂnЪЧЛЅжЪЕФЦцЪ§ЃЎгІгУЃКЕБn=5ЪБЃЌЧѓвЛБпГЄЮЊ12ЕФжБНЧШ§НЧаЮСэСНБпЕФГЄЃЎ
ЃЌЦфжаm>n>0ЃЌmЁЂnЪЧЛЅжЪЕФЦцЪ§ЃЎгІгУЃКЕБn=5ЪБЃЌЧѓвЛБпГЄЮЊ12ЕФжБНЧШ§НЧаЮСэСНБпЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвЪаФГеђзщжЏ20СОЦћГЕзАдЫЭъAЁЂBЁЂCШ§жжЦъГШЙВ100ЖжЕНЭтЕиЯњЪлЃЎАДМЦЛЎЃЌ20СОЦћГЕЖМвЊзАдЫЃЌУПСОЦћГЕжЛФмзАдЫЭЌвЛжжЦъГШЃЌЧвБиаызАТњЃЎИљОнЯТБэЬсЙЉЕФаХЯЂЃЌНтД№вдЯТЮЪЬтЃК
Цъ ГШ ЦЗ жж | A | B | C |
УПСОЦћГЕдЫдиСП(Жж) | 6 | 5 | 4 |
УПЖжЦъГШЛёРћ(АйдЊ) | 12 | 16 | 10 |
(1)ЩшзАдЫAжжЦъГШЕФГЕСОЪ§ЮЊxЃЌзАдЫBжжЦъГШЕФГЕСОЪ§ЮЊyЃЌЧѓyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
(2)ШчЙћзАдЫУПжжЦъГШЕФГЕСОЪ§ЖМВЛЩйгк4СОЃЌФЧУДГЕСОЕФАВХХЗНАИгаМИжжЃПВЂаДГіУПжжАВХХЗНАИЃЛ
(3)ШєвЊЪЙДЫДЮЯњЪлЛёРћзюДѓЃЌгІВЩгУФФжжАВХХЗНАИЃПВЂЧѓГізюДѓРћШѓЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com