
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.

(1)写出四边形![]() 的形状,并证明:
的形状,并证明:
(2)若四边形![]() 的面积为12,
的面积为12,![]() ,求
,求![]() .
.
【答案】(1)详见解析;(2)![]()
【解析】
(1)由“AAS”可证△AEF≌△DEC,可得AF=CD,由直角三角形的性质可得AD=BD=CD,由菱形的判定是可证ADBF是菱形.
(2)由题意可得S△ABC=S四边形ADBF=12,可得AC的长,由勾股定理可求BC的长.
解:解:(1)四边形ADBF是菱形,
理由如下:∵E是AD的中点,
∴AE=DE,
∵AF∥BC
∴∠AFE=∠DCE,且∠AEF=∠CED,AE=DE
∴△AEF≌△DEC(AAS)
∴AF=CD,
∵点D是BC的中点
∴BD=DC
∴AF=BD,且AF∥CD
∴四边形ADBF是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴AD=BD,
∴平行四边形ADBF是菱形
(2)∵四边形ADBF的面积为12,
∴S△ABD=6
∵D是BC的中点
∴S△ABC=12=![]() ×AB×AC
×AB×AC
∴12=![]() ×4×AC
×4×AC
∴AC=6,
∴BC=![]() .
.


科目:初中数学 来源: 题型:
【题目】某校七(1)班学生的平均身高是160厘米,下表给出了该班6名学生的身高情况(单位:厘米).
学 生 | A | B | C | D | E | F |
身 高 | 157 | 162 | 159 | 154 | 163 | 165 |
身高与平均身高的差值 | -3 | +2 | -1 | a | +3 | b |
(1)列式计算表中的数据a和b;
(2)这6名学生中谁最高?谁最矮?最高与最矮学生的身高相差多少?
(3)这6名学生的平均身高与全班学生的平均身高相比,在数值上有什么关系?(通过计算回答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,直线![]() 与
与![]() 轴分别交于点
轴分别交于点![]() 、点
、点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() ,
,![]() 是直线
是直线![]() 上一动点,且在点
上一动点,且在点![]() 的上方,设点
的上方,设点![]() .
.

(1)当四边形![]() 的面积为38时,求点
的面积为38时,求点![]() 的坐标,此时在
的坐标,此时在![]() 轴上有一点
轴上有一点![]() ,在
,在![]() 轴上找一点
轴上找一点![]() ,使得
,使得![]() 最大,求出
最大,求出![]() 的最大值以及此时点
的最大值以及此时点![]() 坐标;
坐标;
(2)在第(1)问条件下,直线![]() 左右平移,平移的距离为
左右平移,平移的距离为![]() . 平移后直线上点
. 平移后直线上点![]() ,点
,点![]() 的对应点分别为点
的对应点分别为点![]() 、点
、点![]() ,当
,当![]() 为等腰三角形时,直接写出
为等腰三角形时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲加工A型零件60个所用时间和乙加工B型零件80个所用时间相同.甲、乙两人每天共加工35个零件,设甲每天加工x个A型零件.
(1)直接写出乙每天加工的零件个数;(用含x的代数式表示)
(2)求甲、乙每天各加工零件多少个?
(3)根据市场预测,加工A型零件所获得的利润为m元/件(3≤m≤5),加工B型零件所获得的利润每件比A型少1元.求甲、乙每天加工的零件所获得的总利润P(元)与m的函数关系式,并求P的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知多项式2x3y﹣xy+16的次数为a,常数项为b,a,b分别对应着数轴上的A、B两点.
(1)a= ,b= ;并在数轴上画出A、B两点;
(2)若点P从点A出发,以每秒3个单位长度单位的速度向x轴正半轴运动,求运动时间为多少时,点P到点A的距离是点P到点B的距离的2倍;
(3)数轴上还有一点C的坐标为30,若点P和Q同时从点A和点B出发,分别以每秒3个单位长度和每秒1个单位长度的速度向C点运动,P到达C点后,再立即以同样的速度返回,运动的终点A,求点P和点Q运动多少秒时,P,Q两点之间的距离为4,并求出此时点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新能源汽车投放市场后,有效改善了城市空气质量。经过市场调查得知,某市去年新能源汽车总量已达到3250辆,预计明年会增长到6370辆.
(1)求今、明两年新能源汽车数量的平均增长率;
(2)为鼓励市民购买新能源汽车,该市财政部门决定对今年增加的新能源汽车给予每辆0.8万元的政府性补贴.在(1)的条件下,求该市财政部门今年需要准备多少补贴资金?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系 xOy 中,正比例函数 y=kx 与一次函数 y=x+b 的图象相交于点 A(4,3).过点 P(2,0)作 x 轴的垂线,分别交正比例函数的图象于点 B,交一次函数的图象于点 C, 连接 OC.
(1)求这两个函数解析式;
(2)求△OBC 的面积;
(3)在 x 轴上是否存在点 M,使△AOM 为等腰三角形? 若存在,直接写出 M 点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解成都市初中学生“数学核心素养”的掌握情况,教育科学院命题教师赴某校初三年级进行调 研,命题教师将随机抽取的部分学生成绩(得分为整数,满分 160 分)分为 5 组:第一组 85~100;第二组100~115;第三组 115~130;第四组 130~145;第五组 145~160,统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图,观察图形的信息,回答下列问题:

(1)本次调查共随机抽取了该年级多少名学生?成绩为第五组的有多少名学生?
(2)针对考试成绩情况,现各组分别派出1名代表(分别用 A、B、C、D、E 表示5个小组中选出来的同学),命题教师从这5名同学中随机选出两名同学谈谈做题的感想,请你用列表或画树状图的方法求出所选两名同学刚好来自第一、五组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
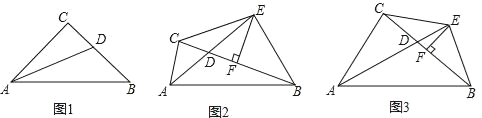
【题目】在△ABC,∠BAC为锐角,AB>AC,AD平分∠BAC交BC于点D.
(1)如图1,若△ABC是等腰直角三角形,直接写出线段AC,CD,AB之间的数量关系;
(2)BC的垂直平分线交AD延长线于点E,交BC于点F.
①如图2,若∠ABE=60°,判断AC,CE,AB之间有怎样的数量关系并加以证明;
②如图3,若AC+AB=![]() AE,求∠BAC的度数.
AE,求∠BAC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com