练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
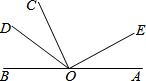
    6．如图∠AOB是平角，过点O作射线OE，OC，OD．把∠BOE用图中的角表示成两个角或三个角和的形式，能有几种不同的表示方法（　　）
    A．2种B．3种C．4种D．5种

    分析 结合图形，根据有公共顶点的两条射线组成的图形是角，可得答案．

    解答 解：∠BOE=∠BOD+∠DOE，∠BOE=∠BOC+∠COE，∠BOE=∠BOD+∠DOC+∠COE，
    共3种，
    故选B．

    点评 本题主要考查了角的定义，结合图形找出相应的角是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    16．多项式-7ab-5a4b+2ab3+9为五次四项式，最高次项系数是-5，常数项是9．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．函数$y=（m-1）{x^{{m^2}-2}}$是反比例函数，则m的值是（　　）
    A．m=±1B．m=1C．m=±$\sqrt{3}$D．m=-1

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．下列各式中，错误的是（　　）
    A．$\sqrt{25}$=5B．±$\sqrt{64}$=±8C．$\sqrt{（-6）^{2}}$=-6D．$\root{3}{-8}$=-2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．计算：
    （1）$\sqrt{16}$-$\sqrt{9}$+$\root{3}{-27}$
    （2）|2-$\sqrt{3}$|+2（$\sqrt{3}$-1）
    （3）$\sqrt{\frac{1}{16}}$-$\sqrt{6\frac{1}{4}}$+|$\sqrt{3}$-π|+$\sqrt{3}$
    （4）$\sqrt{4}$÷2+$\root{3}{27}$×[2-（-$\sqrt{2}$）2]．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．三元一次方程组$\left\{\begin{array}{l}x+y=1\\ y+z=2\\ x+z=3\end{array}\right.$的解是$\left\{\begin{array}{l}{x=1}\\{y=0}\\{z=2}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．如图，O是直线AB上的一点，射线OC，OE分别平分∠AOD和∠BOD．
    （1）与∠COD相等的角有∠AOC；
    （2）与∠AOC互余的角有∠BOE，∠DOE；
    （3）已知∠AOC=58°，求∠BOE的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．已知：如图，在直角梯形纸片ABCD中，DC∥AB，AB＞CD＞AD，∠A=90°，将纸片沿过点D的直线翻折，使点A落在边CD上的点E处，折痕为DF，联结EF并展开纸片．
    （1）求证：四边形ADEF为正方形；
    （2）取线段AF的中点G，联结GE，当BG=CD时，求证：四边形GBCE为等腰梯形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．已知扇形的半径为3，圆心角为120°，它的弧长为2π．

    查看答案和解析>>

    同步练习册答案