
【题目】在平面直角坐标系![]() 中,对于任意一点
中,对于任意一点![]() ,定义点
,定义点![]() 的“离心值”
的“离心值”![]() 为:
为: 时,例如对于点
时,例如对于点![]() ,因为
,因为![]() ,所以
,所以![]() .
.
解决下列问题:
(1)已知![]() ,
,![]() ,
,![]() ,直接写出
,直接写出![]() 的值,并将
的值,并将![]() ,
,![]() ,
,![]() 按从小到大的顺序排列(用“<”连接);
按从小到大的顺序排列(用“<”连接);
(2)如图,点![]() ,线段
,线段![]() 上的点
上的点![]() ,
,
①若![]() ,求点
,求点![]() 的坐标;
的坐标;
②在图中画出满足![]() 的点
的点![]() 组成的图形,并用语言描述该图形的特征;
组成的图形,并用语言描述该图形的特征;

科目:初中数学 来源: 题型:
【题目】对于气温,有的地方用摄氏度表示,有的地方用华氏温度表示,从温度计上可以看出,摄氏温度![]() 与华氏温度
与华氏温度![]() 有如下对应的关系.下列说法不正确的是( )
有如下对应的关系.下列说法不正确的是( )

A. 摄氏温度![]() 与华氏温度
与华氏温度![]() 都是变量,摄氏温度
都是变量,摄氏温度![]() 是自变量,华氏温度
是自变量,华氏温度![]() 是因变量
是因变量
B. 随着摄氏温度![]() 的逐渐升高,华氏温度
的逐渐升高,华氏温度![]() 也逐新升高
也逐新升高
C. 摄氏温度每升高![]() ,华氏温度升高
,华氏温度升高![]()
D. 当摄氏温度为![]() 时,华氏温度为
时,华氏温度为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划组织师生共300人参加一次大型公益活动,如果租用6辆大客车和5辆小客车,恰好全部坐满,已知每辆大客车的乘客座位数比小客车多17个.
(1)求每辆大客车和每辆小客车的乘客座位数;
(2)由于最后参加活动的人数增加了30人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,且所有参加活动的师生都有座位,求租用小客车数量的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)用方程解答下列问题
(1)一个角的余角比它的补角的![]() 还少15°,求这个角的度数.
还少15°,求这个角的度数.
(2)几个人共同搬运一批货物,如果每人搬运8箱货物,则剩下7箱货物未搬运;如果每人搬运12箱货物,则缺13箱货物,求参与搬运货物的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() ,点
,点![]() 是平面上一点,射线
是平面上一点,射线![]() 与直线
与直线![]() 交于点
交于点![]() ,射线
,射线![]() 与直线
与直线![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() ,
,![]() 与
与![]() 所在的直线交于点
所在的直线交于点![]() .
.
(1)如图1,当![]() ,
,![]() 时,写出
时,写出![]() 的一个余角,并证明
的一个余角,并证明![]() ;
;
(2)若![]() ,
,![]() .
.
①如图2,当点![]() 在
在![]() 内部时,用等式表示
内部时,用等式表示![]() 与
与![]() 之间的数量关系,并加以证明;
之间的数量关系,并加以证明;
②如图3,当点![]() 在
在![]() 外部时,依题意补全图形,并直接写出用等式表示的
外部时,依题意补全图形,并直接写出用等式表示的![]() 与
与![]() 之间的数量关系.
之间的数量关系.


查看答案和解析>>
科目:初中数学 来源: 题型:
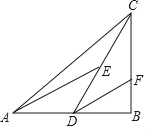
【题目】定义:有两条边长的比值为![]() 的直角三角形叫“潜力三角形”.如图,在△ABC中,∠B=90°,D是AB的中点,E是CD的中点,DF∥AE交BC于点F.
的直角三角形叫“潜力三角形”.如图,在△ABC中,∠B=90°,D是AB的中点,E是CD的中点,DF∥AE交BC于点F.
(1)设“潜力三角形”较短直角边长为a,斜边长为c,请你直接写出![]() 的值为 ;
的值为 ;
(2)若∠AED=∠DCB,求证:△BDF是“潜力三角形”;
(3)若△BDF是“潜力三角形”,且BF=1,求线段AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
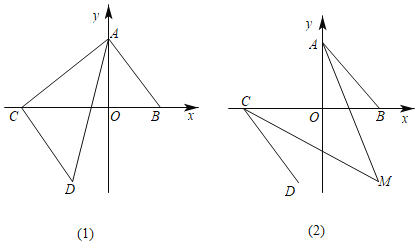
【题目】如图,在平面直角坐标系中,已知点A(0,4),B(3,0),线段AB平移后对应的线段为CD,点C在x轴的负半轴上,B、C两点之间的距离为8.
(1)求点D的坐标;
(2)如图(1),求△ACD的面积;
(3)如图(2),∠OAB与∠OCD的角平分线相交于点M,探求∠AMC的度数并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图).已知该材料初始温度是32℃.
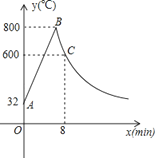
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作.那么锻造的操作时间有多长?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com