
【题目】已知∠MON=45°,其内部有一点P关于OM的对称点是A,关于ON的对称点是B,且OP=2cm,则S△AOB= .
【答案】2cm2
【解析】解:∵点P关于OM的对称点是A, ∴OA=OP,∠AOM=∠MOP,
∵点P关于ON的对称点是B,
∴OB=OP,∠BON=∠BOP,
∴OA=OB=OP,∠AOB=∠AOM+∠MOP+∠BON+∠BOP=2(∠MOP+∠NOP)=2∠MON=2×45°=90°,
∴△AOB是等腰直角三角形,
∵OP=2cm,
∴S△AOB= ![]() ×22=2cm2 .
×22=2cm2 .
所以答案是:2cm2 . 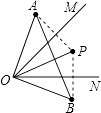
【考点精析】掌握等腰直角三角形和轴对称的性质是解答本题的根本,需要知道等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;关于某条直线对称的两个图形是全等形;如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线;两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上.


 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于E. 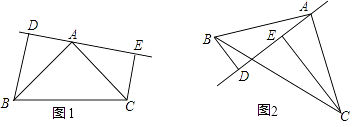
(1)若BC在DE的同侧(如图1)且AD=CE,请写出:BA和AC的位置关系 . (不必证明)
(2)若BC在DE的两侧(如图2)其他条件不变,请问(1)中AB与AC的位置关系还成立吗?若成立,写出证明过程;若不成立,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分7分) 已知:如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=![]() OB.
OB.
(1)求证:AB是⊙O的切线;
(2)若∠ACD=45°,OC=2,求弦CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC中,AB=AC=6,BC=4,∠A=40°. 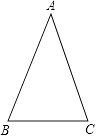
(1)用尺规作出边AB的垂直平分线交AB于点D,交AC于点E(不写作法,保留作图痕迹,并在图中标注字母).
(2)连接BE,求△EBC的周长和∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
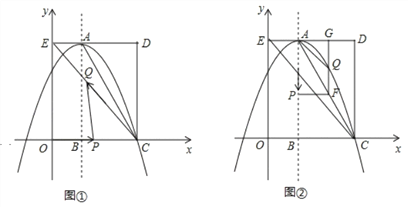
【题目】如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.
(1)填空:点A坐标为 ;抛物线的解析式为 .
(2)在图1中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在图2中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com