
【题目】如图,在直角坐标系中,△ABC是格点三角形(三角形的三个顶点都是小正方形的顶点).
(1)在第一象限内找一点P,以格点P、A、B为顶点的三角形与△ABC相似但不全等,请写出符合条件格点P的坐标;
(2)请用直尺与圆规在第一象限内找到两个点M、N,使∠AMB=∠ANB=∠ACB.请保留作图痕迹,不要求写画法.

【答案】(1)P(1,4)或P′(3,4);(2)见解析.
【解析】试题分析:
(1)分△APB∽△ABC,△BPA∽△ABC,△BAP∽△ABC三种情况分析讨论,并把全等的情况去掉即可;
(2)根据同弧所对的圆周角相等,以BC为直径作Rt△ABC的外接圆即可找到符合条件的点M、N.
试题解析:
(1)如图1所示:
当△AP1B∽△ABC时,P1A:AB=AC:AB=1:2,解得P1A=4,此时点P的坐标为(1,4);
当△BP2A∽△ABC时,P2B:AB=AB:AC=2:1,解得P2B=4,此时点P的坐标为(3,4);
当△BAP3∽△ABC时,P3B:AB=AC:AB=1:2,解得P3B=1,此时两三角形全等,不符合题意,舍去;
综上所述,点P的坐标为(1,4)或(3,4);

(2)如图,作△ABC的外接圆,在![]() 上取两点M,N即可.
上取两点M,N即可.



科目:初中数学 来源: 题型:
【题目】如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处;
(1)求证:B′E=BF;
(2)设AE=a,AB=b,BF=C,试猜想a,b,c之间的一种关系,并给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
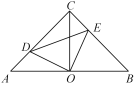
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,O是AB的中点,点D在AC上,点E在BC上,且∠DOE=90°.则下列结论:①OA=OB=OC;②CD=BE;③△ODE是等腰直角三角形;④四边形CDOE的面积等于△ABC的面积的一半.其中正确的有____(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解
如图1,已知点A是BC外一点,连接AB,AC,求∠BAC+∠B+∠C的度数.
(1)阅读并补充下面推理过程
解:过点A作ED∥BC
∴∠B=∠ ,∠C=∠ .
又∵∠EAB+∠BAC+∠DAC=180°(平角定义)
∴∠B+∠BAC+∠C=180°
从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将∠BAC,∠B,∠C“凑”在一起,得出角之间的关系,使问题得以解决
(2)如图2,已知AB∥ED,求∠B+∠BCD+∠D的度数.
小明受到启发,过点C作CF∥AB如图所示,请你帮助小明完成解答:
(3)已知AB∥CD,点C在点D的右侧,∠ADC=70°.BE平分∠ABC,DE平分∠ADC,BE,DE所在的直线交于点E,点E在AB与CD两条平行线之间.
①如图3,点B在点A的左侧,若∠ABC=60°,则∠BED的度数为 °.
②如图4,点B在点A的右侧,且AB<CD,AD<BC.若∠ABC=n°,则∠BED的度数为 °(用含n的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC交BC于点D,AE⊥BC,垂足为E,且CF∥AD.

(1)如图1,若△ABC是锐角三角形,∠B=30°,∠ACB=70°,则∠CFE= 度;
(2)若图1中的∠B=x,∠ACB=y,则∠CFE= ;(用含x、y的代数式表示)
(3)如图2,若△ABC是钝角三角形,其他条件不变,则(2)中的结论还成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC=∠ACD=90°,∠ABC=∠ADC,CE⊥AD,且BE平分∠ABC,则下列结论:①AD=BC;②∠ACE=∠ABC;③∠ECD+∠EBC=∠BEC;④∠CEF=∠CFE.其中正的是( )

A. ①②B. ①③④C. ①②④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32,连接BD,AE⊥BD,垂足为E.
(1)求证:△ABE∽△DBC;
(2)求线段AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.
(1)请猜想:DC与BE的数量关系,并给予证明;
(2)求证:DC⊥BE.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com