【题目】两个大小不同的等腰直角三角形三角板如图1所示放置，图2是由它抽象出的几何图形，B，C，E在同一条直线上，连结DC．

（1）请猜想：DC与BE的数量关系，并给予证明；

（2）求证：DC⊥BE．

参考答案：

【答案】（1）DC＝BE；（2）详见解析;

【解析】

（1）根据等腰直角三角形的性质，可以得出△ABE≌△ACD，得出对应边相等即可；

（2）由△ABE≌△ACD可以得出∠B=∠ACD=45°，进而得出∠DCB=90°，就可以得出结论．

（1）解：DC＝BE；

理由如下：∵△ABC与△AED均为等腰直角三角形，

∴AB＝AC，AE＝AD，∠BAC＝∠EAD＝90°．∠ABC＝∠ACB＝45°，

∴∠BAC+∠CAE＝∠EAD+∠CAE．

即∠BAE＝∠CAD，

在△ABE与△ACD中，，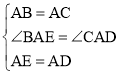

∴△ABE≌△ACD（SAS），

∴DC＝BE；

（2）证明：∵△ABE≌△ACD，

∴∠ACD＝∠ABE＝45°，

又∵∠ACB＝45°，

∴∠BCD＝∠ACB+∠ACD＝90°，

∴DC⊥BE．

关闭