练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

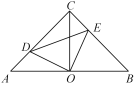
    【题目】如图，在△ABC中，∠ACB＝90°，AC＝BC，O是AB的中点，点D在AC上，点E在BC上，且∠DOE＝90°.则下列结论：①OA＝OB＝OC；②CD＝BE；③△ODE是等腰直角三角形；④四边形CDOE的面积等于△ABC的面积的一半.其中正确的有____(填序号).

    【答案】①②③④

    【解析】

    根据直角三角形斜边上的中线等于斜边的一半来判定①；证明△COD≌△BOE，来判定②③④；

    解：在△ABC中，∵∠ACB＝90°，AC＝BC，O是AB的中点，

    ∴OA＝OB＝OC；故①正确；

    ∵AC＝BC，O是AB的中点，∴OC⊥AB,

    ∵∠DOE＝∠COB=90°

    ∴∠DOC=∠EOB,

    又∵OC=OB,∠DCO=∠EBO=45°，

    ∴△COD≌△BOE．

    ∴CD=EB,OD=OE,S△COD =S△BOE,即②③④正确.

    故答案为：①②③④.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知一次函数y＝kx+b的图象经过点（0，2）和点（1，﹣1）．

    （1）求这个一次函数的解析式；

    （2）求此一次函数图象与两坐标轴所围成的三角形面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

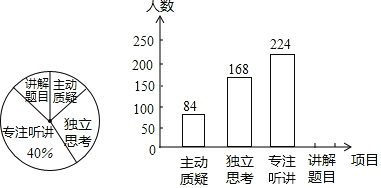
    【题目】某市数学调研小组对老师在讲评试卷中学生参与的深度与广度进行评价调查，其评价项目为“主动质疑”、“独立思考”、“专注听讲”、“讲解题目”四项，该调研小组随机抽取了若干名初中七年级学生的参与情况，绘制成如图所示的频数分布直方图和扇形統计图（均不完整），请根据图中所给信息答下列问题：

    （1）在这次评价中，一共抽查了　　名学生；

    （2）请将频数分布直方图补充完整；

    （3）如果全市有4000名七年级学生，那么在试卷评讲课中，“独立思考”的七年级学生约有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，平行四边形ABCD中，E，F是对角线BD上的两点，如果添加一个条件使△ABE≌△CDF，则添加的条件不能是( )

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示,在△ABC中,AB∶BC∶CA=3∶4∶5,且周长为36 cm,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,则过3s时,△BPQ的面积为____cm2.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知有一块等腰三角形纸板，在它的两腰上各有一点E和F，把这两点分别与底边中点连结，并沿着这两条线段剪下两个三角形，所得的这两个三角形相似，剩余部分（四边形）的四条边的长度如图所示，那么原等腰三角形的底边长为（　　）

    A. B. C. 或 D. 或

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在直角坐标系中，△ABC是格点三角形（三角形的三个顶点都是小正方形的顶点）．

    （1）在第一象限内找一点P，以格点P、A、B为顶点的三角形与△ABC相似但不全等，请写出符合条件格点P的坐标；

    （2）请用直尺与圆规在第一象限内找到两个点M、N，使∠AMB=∠ANB=∠ACB．请保留作图痕迹，不要求写画法．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】请将下列证明过程补充完整：

    已知：如图，AE平分∠BAC，CE平分∠ACD,且∠α＋∠β＝90°.

    求证：AB∥CD.

    证明：∵CE平分∠ACD (已知），

    ∴∠ACD＝2∠α(______________________)

    ∵AE平分∠BAC (已知)，

    ∴∠BAC＝_________(______________________)

    ∵∠α＋∠β＝90°（已知），

    ∴2∠α＋2∠β＝180°（等式的性质）

    ∴∠ACD＋∠BAC＝＝_________(______________________)

    ∴AB∥CD.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠BAC＝∠ACD＝90°，∠ABC＝∠ADC，CE⊥AD，且BE平分∠ABC，则下列结论：①AD＝BC；②∠ACE＝∠ABC；③∠ECD＋∠EBC＝∠BEC；④∠CEF＝∠CFE．其中正的是（ ）

    A. ①②B. ①③④C. ①②④D. ①②③④

    查看答案和解析>>

    同步练习册答案