
【题目】请将下列证明过程补充完整:
已知:如图,AE平分∠BAC,CE平分∠ACD,且∠α+∠β=90°.
求证:AB∥CD.
证明:∵CE平分∠ACD (已知),
∴∠ACD=2∠α(______________________)
∵AE平分∠BAC (已知),
∴∠BAC=_________(______________________)
∵∠α+∠β=90°(已知),
∴2∠α+2∠β=180°(等式的性质)
∴∠ACD+∠BAC==_________(______________________)
∴AB∥CD.

【答案】角平分线的定义,2∠β,等式性质,180°,等量代换,同旁内角互补,两直线平行.
【解析】
先根据角平分线的定义,得到∠ACD+∠BAC=2∠α+2∠β,再根据∠α+∠β=90°,即可得到∠ACD+∠BAC=180°,进而判定AB∥CD.
解答:证明:∵CE平分∠ACD (已知),
∴∠ACD=2∠α (角平分线的定义).
∵AE平分∠BAC (已知),
∴∠BAC=2∠β(角的平分线的定义).
∴∠ACD+∠BAC=2∠α+2∠β(等式性质).
即∠ACD+∠BAC=2(∠α+∠β).
∵∠α+∠β=90° (已知),
∴∠ACD+∠BAC=180° (等量代换).
∴AB∥CD(同旁内角互补,两直线平行).
故答案为:角平分线的定义,2∠β,等式性质,180°,等量代换,同旁内角互补,两直线平行.


科目:初中数学 来源: 题型:
【题目】5月13日,周杰伦2017“地表最强”世界巡回演唱会在奥体中心盛大举行,1号巡逻员从舞台走往看台,2号巡逻号从看台走往舞台,两人同时出发,分别以各自的速度在舞台与看台间匀速走动,出发1分钟后,1号巡逻员发现对讲机遗忘在出发地,便立即返回出发地,拿到对讲机后(取对讲机时间不计)立即再从舞台走往看台,结果1号巡逻员先到达看台,2号巡逻员继续走到舞台,设2号巡逻员的行驶时间为x(min),两人之间的距离为y(m),y与x的函数图象如图所示,则当1号巡逻员到达看台时,2号巡逻员离舞台的距离是________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
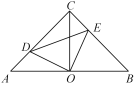
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,O是AB的中点,点D在AC上,点E在BC上,且∠DOE=90°.则下列结论:①OA=OB=OC;②CD=BE;③△ODE是等腰直角三角形;④四边形CDOE的面积等于△ABC的面积的一半.其中正确的有____(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC交BC于点D,AE⊥BC,垂足为E,且CF∥AD.

(1)如图1,若△ABC是锐角三角形,∠B=30°,∠ACB=70°,则∠CFE= 度;
(2)若图1中的∠B=x,∠ACB=y,则∠CFE= ;(用含x、y的代数式表示)
(3)如图2,若△ABC是钝角三角形,其他条件不变,则(2)中的结论还成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC=∠ACD=90°,∠ABC=∠ADC,CE⊥AD,且BE平分∠ABC,则下列结论:①AD=BC;②∠ACE=∠ABC;③∠ECD+∠EBC=∠BEC;④∠CEF=∠CFE.其中正的是( )

A. ①②B. ①③④C. ①②④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,M、N是BD的三等分点,连接CM并延长交AB于点E,连接EN并延长交CD于点F,以下结论:
①E为AB的中点;
②FC=4DF;
③S△ECF=![]() ;
;
④当CE⊥BD时,△DFN是等腰三角形.
其中一定正确的是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32,连接BD,AE⊥BD,垂足为E.
(1)求证:△ABE∽△DBC;
(2)求线段AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2,若S=2,则S1+S2=( )

A. 4 B. 6 C. 8 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知线段![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,如图1所示.
,如图1所示.

(1)平移线段![]()
![]() 到线段
到线段![]()
![]() ,使点
,使点![]() 的对应点为,点
的对应点为,点![]() 的对应点为
的对应点为![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)平移线段![]()
![]() 到线段
到线段![]()
![]() ,使点
,使点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在第二象限内(
在第二象限内(![]() 与
与![]() 对应,
对应, ![]() 与
与![]() 对应),连接
对应),连接![]() 如图2所示.若
如图2所示.若![]() 表示△BCD的面积),求点
表示△BCD的面积),求点![]() 、
、![]() 的坐标;
的坐标;
(3)在(2)的条件下,在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使
,使![]() 表示△PCD的面积)?若存在,求出点
表示△PCD的面积)?若存在,求出点![]() 的坐标; 若不存在,请说明理由.
的坐标; 若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com