
【题目】在平面直角坐标系中,已知线段![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,如图1所示.
,如图1所示.

(1)平移线段![]()
![]() 到线段
到线段![]()
![]() ,使点
,使点![]() 的对应点为,点
的对应点为,点![]() 的对应点为
的对应点为![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)平移线段![]()
![]() 到线段
到线段![]()
![]() ,使点
,使点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在第二象限内(
在第二象限内(![]() 与
与![]() 对应,
对应, ![]() 与
与![]() 对应),连接
对应),连接![]() 如图2所示.若
如图2所示.若![]() 表示△BCD的面积),求点
表示△BCD的面积),求点![]() 、
、![]() 的坐标;
的坐标;
(3)在(2)的条件下,在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使
,使![]() 表示△PCD的面积)?若存在,求出点
表示△PCD的面积)?若存在,求出点![]() 的坐标; 若不存在,请说明理由.
的坐标; 若不存在,请说明理由.
科目:初中数学 来源: 题型:
【题目】请将下列证明过程补充完整:
已知:如图,AE平分∠BAC,CE平分∠ACD,且∠α+∠β=90°.
求证:AB∥CD.
证明:∵CE平分∠ACD (已知),
∴∠ACD=2∠α(______________________)
∵AE平分∠BAC (已知),
∴∠BAC=_________(______________________)
∵∠α+∠β=90°(已知),
∴2∠α+2∠β=180°(等式的性质)
∴∠ACD+∠BAC==_________(______________________)
∴AB∥CD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC=∠ACD=90°,∠ABC=∠ADC,CE⊥AD,且BE平分∠ABC,则下列结论:①AD=BC;②∠ACE=∠ABC;③∠ECD+∠EBC=∠BEC;④∠CEF=∠CFE.其中正的是( )

A. ①②B. ①③④C. ①②④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥DE,∠B=60°,AE⊥BC,垂足为点E.
(1)求∠AED的度数;
(2)当∠EDC满足什么条件时,AE∥DC,证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将背面完全相同,正面上分别写有数字1,2,3,4的四张卡片混合后,小明从中随机地抽取一张,把卡片上的数字做为被减数,将形状、大小完全相同,分别标有数字1,2,3的三个小球混合后,小华从中随机地抽取一个,把小球上的数字做为减数,然后计算出这两个数的差.
(1)请你用画树状图或列表的方法,求这两数差为0的概率;
(2)小明与小华做游戏,规则是:若这两数的差为非负数,则小明赢;否则,小华赢.你认为该游戏公平吗?请说明理由.如果不公平,请你修改游戏规则,使游戏公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形BCDE的各边分别平行于x轴与y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2018次相遇地点的坐标是( )

A. (1,﹣1) B. (2,0) C. (﹣1,1) D. (﹣1,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C,D是AB的垂直平分线上两点,延长AC,DB交于点E,AF∥BC交DE于点F.
求证:(1)AB是∠CAF的角平分线;
(2)∠FAD = ∠E.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线l1:y=2x+8与坐标轴分别交于A,B两点,点C在x正半轴上,且OA=OC.点P为线段AC(不含端点)上一动点,将线段OP绕点O逆时针旋转90°,得线段OQ(见图2)
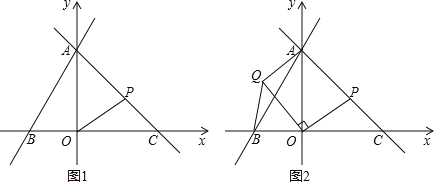
(1)分别求出点B、点C的坐标;
(2)如图2,连接AQ,求证:∠OAQ=45°;
(3)如图2,连接BQ,试求出当线段BQ取得最小值时点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com