
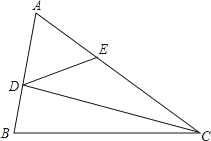
【题目】在△ABC中,已知∠CAB=60°,D、E分别是边AB、AC上的点,且∠AED=60°,ED+DB=CE,∠CDB=2∠CDE,则∠DCB等于_____.
【答案】20°.
【解析】
延长AB到F使BF=AD,连接CF,如图,先判断△ADE为等边三角形得到AD=DE=AE,∠ADE=60°,再利用∠CDB=2∠CDE得到∠CDE=40°,∠CDB=80°,接着证明AF=AC,从而可判断△AFC为等边三角形,则有CF=AC,∠F=60°,然后证明△ACD≌△FCB 得到CB=CD,最后根据等腰三角形的性质和三角形内角和计算∠DCB的度数.
延长AB到F使BF=AD,连接CF,如图,

∵∠CAD=60°,∠AED=60°,
∴△ADE为等边三角形,
∴AD=DE=AE,∠ADE=60°,
∴∠BDE=180°﹣∠ADE=120°,
∵∠CDB=2∠CDE,
∴3∠CDE=120°,解得∠CDE=40°,
∴∠CDB=2∠CDE=80°,
∵BF=AD,
∴BF=DE,
∵DE+BD=CE,
∴BF+BD=CE,即DF=CE,
∵AF=AD+DF,AC=AE+CE,
∴AF=AC,
而∠BAC=60°,
∴△AFC为等边三角形,
∴CF=AC,∠F=60°,
在△ACD和△FCB 中
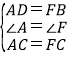 ,
,
∴△ACD≌△FCB(SAS),
∴CB=CD,
∴∠CBD=∠CDB=80°,
∴∠DCB=180﹣(∠CBD+∠CDB)=20°.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】小虫从某点![]() 点处出发在一直线上来回爬行,假定向右爬行的路程记为正数,左爬行的路程为负数,爬行的路程依次为(单位:厘米):+5,-3,+10,-8,-6,+12,-11.
点处出发在一直线上来回爬行,假定向右爬行的路程记为正数,左爬行的路程为负数,爬行的路程依次为(单位:厘米):+5,-3,+10,-8,-6,+12,-11.
(1)小虫最后是否回到出发点![]() 点?如果不在,请说出小虫的位置;
点?如果不在,请说出小虫的位置;
(2)小虫离开出发点![]() 点最远时是 厘米;
点最远时是 厘米;
(3)在爬行过程中,如果每爬1厘米奖励两粒芝麻,则小虫共得多少粒芝麻?
查看答案和解析>>
科目:初中数学 来源: 题型:
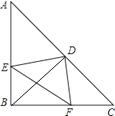
【题目】如图,在等腰直角三角形ABC中,∠ABC=90°,D为AC边中点,过D点作DE⊥DF,交AB于E,交BC于F,连接BD.
(1)求证:△CDF≌△BED
(2)若AE=4,FC=3,求AB长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程![]() .
.
(1)求证:无论k为何值,方程总有实数根.
(2)设![]() 是方程
是方程![]() 的两个根,记
的两个根,记![]() ,S的值能为2吗?若能,求出此时k的值;若不能,请说明理由.
,S的值能为2吗?若能,求出此时k的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=mx+n与反比例函数交于A、B两点,点A在点B的左边,与x轴、y轴分别交于点C、点D,AE⊥x轴于E,BF⊥y轴于F
(1) 若m=k,n=0,求A,B两点的坐标(用m表示).
(2) 如图1,若A(x1,y1)、B(x2,y2),写出y1+y2与n的大小关系,并证明.
(3) 如图2,M、N分别为反比例函数![]() 图象上的点,AM∥BN∥x轴.若
图象上的点,AM∥BN∥x轴.若![]() ,且AM,BN之间的距离为5,则k-b=_____________
,且AM,BN之间的距离为5,则k-b=_____________

查看答案和解析>>
科目:初中数学 来源: 题型:
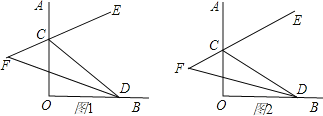
【题目】如图,∠AOB=90°,点C、D分别在射线OA、OB上,CE是∠ACD的平分线,CE的反向延长线与∠CDO的平分线交于点F.
(1)当∠OCD=50°(图1),试求∠F.
(2)当C、D在射线OA、OB上任意移动时(不与点O重合)(图2),∠F的大小是否变化?若变化,请说明理由;若不变化,求出∠F.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算并观察下列各式:
第1个:(a﹣b)(a+b)=______;
第2个:(a﹣b)(a2+ab+b2)=______;
第3个:(a﹣b)(a3+a2b+ab2+b3)=_______;
……
这些等式反映出多项式乘法的某种运算规律.
(2)猜想:若n为大于1的正整数,则(a﹣b)(an﹣1+an﹣2b+an﹣3b2+……+a2bn﹣3+abn﹣2+bn﹣1)=________;
(3)利用(2)的猜想计算:2n﹣1+2n﹣2+2n﹣3+……+23+22+1=______.
(4)拓广与应用:3n﹣1+3n﹣2+3n﹣3+……+33+32+1=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD中,EF分别是AB、AD边上的点,DE与CF交于点G.
(1)如图1,若四边形ABCD是正方形,且DE⊥CF,求证:DE=CF;
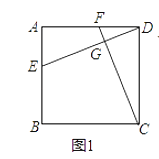
(2)如图2,若四边形ABCD是矩形,且DE⊥CF,求证:![]() ;
;
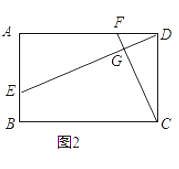
(3)如图3,若四边形ABCD是平行四边形,当∠B=∠EGF时,第(2)问的结论是否成立?若成立给予证明;若不成立,请说明理由.
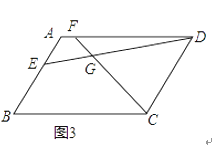
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校要从小王和小李两名同学中挑选一人参加全国数学竞赛,在最近的五次选拔测试中,他俩的成绩分别如下表:

根据上表解答下列问题:
(1)完成下表:
姓名 | 极差(分) | 平均成绩(分) | 中位数(分) | 众数(分) | 方差 |
小王 | 40 | 80 | 75 | 75 | 190 |
小李 |
(2)在这五次测试中,成绩比较稳定的同学是谁?若将80分以上(含80分)的成绩视为优秀,则小王、小李在这五次测试中的优秀率各是多少?
(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获得一等奖,那么你认为应选谁参加比赛比较合适?说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com