
【题目】已知关于x的方程![]() .
.
(1)求证:无论k为何值,方程总有实数根.
(2)设![]() 是方程
是方程![]() 的两个根,记
的两个根,记![]() ,S的值能为2吗?若能,求出此时k的值;若不能,请说明理由.
,S的值能为2吗?若能,求出此时k的值;若不能,请说明理由.
【答案】(1)证明见解析;(2)S的值能为2,此时k的值为2.
【解析】
试题(1)分两种情况讨论:①当k=1时,方程是一元一次方程,有实数根;②当k≠1时,方程是一元二次方程,所以证明判别式是非负数即可;
(2)由韦达定理得![]() ,
,![]() ,代入到
,代入到![]() =2中,可求得k的值.
=2中,可求得k的值.
试题解析:(1)当k=1时,原方程可化为2x+2=0,解得:x=﹣1,此时该方程有实根;
当k≠1时,方程是一元二次方程,∵△=![]() =
=![]() =
=![]() >0,∴无论k为何实数,方程总有实数根,综上所述,无论k为何实数,方程总有实数根.
>0,∴无论k为何实数,方程总有实数根,综上所述,无论k为何实数,方程总有实数根.
(2)由根与系数关系可知,![]() ,
,![]() ,若S=2,则
,若S=2,则![]() =2,即
=2,即![]() ,将
,将![]() 、
、![]() 代入整理得:
代入整理得:![]() ,解得:k=1(舍)或k=2,∴S的值能为2,此时k=2.
,解得:k=1(舍)或k=2,∴S的值能为2,此时k=2.


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:
【题目】已知:点C、A、D在同一条直线上,∠ABC=∠ADE=α,线段 BD、CE交于点M.
(1)如图1,若AB=AC,AD=AE
①问线段BD与CE有怎样的数量关系?并说明理由;
②求∠BMC的大小(用α表示);
(2)如图2,若AB= BC=kAC,AD =ED=kAE则线段BD与CE的数量关系为 ,∠BMC= (用α表示);
(3)在(2)的条件下,把△ABC绕点A逆时针旋转180°,在备用图中作出旋转后的图形(要求:尺
规作图,不写作法,保留作图痕迹),连接 EC并延长交BD于点M.则∠BMC= (用α表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程![]() ,下列说法正确的是( )
,下列说法正确的是( )
A. 当k=0时,方程没有实数根 B. 当k=1时,方程有一个实数根
C. 当k=-1时,方程有两个相等的实数根 D. 当k≠0时,方程总有两个不相等的实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式:![]() ,
,![]() .给出定义如下:使等式
.给出定义如下:使等式![]() 成立的一对有理数
成立的一对有理数![]() ,
,![]() 为“共生有理数对”,记为
为“共生有理数对”,记为![]() .如:数对
.如:数对![]() ,
,![]() 都有“共生有理数对”.
都有“共生有理数对”.
(1)数对![]() ,
,![]() 中是“共生有理数对”的是 .
中是“共生有理数对”的是 .
(2)请再写出另外一对符合条件的“共生有理数对” (不能与题目中已有的重复).
(3)小丁说:“若![]() 是‘共生有理数对’,则
是‘共生有理数对’,则![]() 一定是‘共生有理数对’.”请你用(2)中写出的“共生有理数对”验证小丁的说法.
一定是‘共生有理数对’.”请你用(2)中写出的“共生有理数对”验证小丁的说法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,已知∠CAB=60°,D、E分别是边AB、AC上的点,且∠AED=60°,ED+DB=CE,∠CDB=2∠CDE,则∠DCB等于_____.
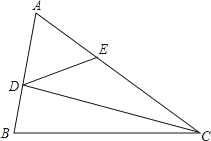
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC的三个内角A,B,C所对的边分别是![]() ,下列条件中,不能判定△ABC是等腰三角形的是( )
,下列条件中,不能判定△ABC是等腰三角形的是( )
A.a3,b3,c4B.a︰b︰c2︰3︰4
C.∠B50°,∠C80°D.∠A︰∠B︰∠C1︰1︰2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师请同学思考如下问题:如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗?
小敏在思考问题时,有如下思路:连接AC.

结合小敏的思路作答:
(1)若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?说明理由,参考小敏思考问题的方法解决一下问题;
(2)如图2,在(1)的条件下,若连接AC,BD.
①当AC与BD满足什么条件时,四边形EFGH是菱形,写出结论并证明;
②当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com