
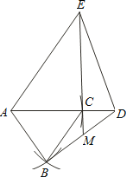
【题目】已知:点C、A、D在同一条直线上,∠ABC=∠ADE=α,线段 BD、CE交于点M.
(1)如图1,若AB=AC,AD=AE
①问线段BD与CE有怎样的数量关系?并说明理由;
②求∠BMC的大小(用α表示);
(2)如图2,若AB= BC=kAC,AD =ED=kAE则线段BD与CE的数量关系为 ,∠BMC= (用α表示);
(3)在(2)的条件下,把△ABC绕点A逆时针旋转180°,在备用图中作出旋转后的图形(要求:尺
规作图,不写作法,保留作图痕迹),连接 EC并延长交BD于点M.则∠BMC= (用α表示).

【答案】(1)①BD=CE,理由见解析②180°-2α(2)BD=kCE,![]() α(3)
α(3)![]()
【解析】解:(1)如图1。
①BD=CE,理由如下:
∵AD=AE,∠ADE=α,∴∠AED=∠ADE=α,。∴∠DAE=180°-2∠ADE=180°-2α。同理可得:∠BAC=180°-2α。∴∠DAE=∠BAC。
∴∠DAE+∠BAE=∠BAC+∠BAE,即:∠BAD=∠CAE。
在△ABD与△ACE中,∵AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE(SAS)。∴BD=CE。
②∵△ABD≌△ACE,∴∠BDA=∠CEA。
∵∠BMC=∠MCD+∠MDC,∴∠BMC=∠MCD+∠CEA=∠DAE=180°-2α。
(2)如图2,BD=kCE,![]() α。
α。
(3)作图如下:
![]() 。
。
(1)①先根据等腰三角形等角对等边的性质及三角形内角和定理得出∠DAE=∠BAC,则∠BAD=∠CAE,再根据SAS证明△ABD≌△ACE,从而得出BD=CE。
②先由全等三角形的对应角相等得出∠BDA=∠CEA,再根据三角形的外角性质即可得出
∠BMC=∠DAE=180°-2α。
(2)∵AD=ED,∠ADE=α,∴∠DAE=![]() 。
。
同理可得:∠BAC=![]() 。
。
∴∠DAE=∠BAC。
∴∠DAE+∠BAE=∠BAC+∠BAE,即:∠BAD=∠CAE。
∵AB=kAC,AD=kAE,∴AB:AC=AD:AE=k。
在△ABD与△ACE中,∵AB:AC=AD:AE=k,∠BDA=∠CEA,∴△ABD∽△ACE。
∴BD:CE=AB:AC=AD:AE=k,∠BDA=∠CEA。∴BD=kCE。
∵∠BMC=∠MCD+∠MDC,∴∠BMC=∠MCD+∠CEA=∠DAE=![]() 。
。
(3)先在备用图中利用SSS作出旋转后的图形,再根据等腰三角形等角对等边的性质及三角形内角和定理得出∠DAE=∠BAC=![]() ,由AB=kAC,AD=kAE,得出AB:AC=AD:AE=k,从而证出△ABD∽△ACE,得出∠BDA=∠CEA,然后根据三角形的外角性质即可得出∠BMC=
,由AB=kAC,AD=kAE,得出AB:AC=AD:AE=k,从而证出△ABD∽△ACE,得出∠BDA=∠CEA,然后根据三角形的外角性质即可得出∠BMC=![]() :
:
∵AD=ED,∠ADE=α,∴∠DAE=∠AED=![]() 。
。
同理可得:∠BAC=![]() 。
。
∴∠DAE=∠BAC,即∠BAD=∠CAE。
∵AB=kAC,AD=kAE,∴AB:AC=AD:AE=k。
在△ABD与△ACE中,∵AB:AC=AD:AE=k,∠BAD=∠CAE,∴△ABD∽△ACE。
∴∠BDA=∠
∵∠BMC=∠MCD+∠MDC,∠MCD=∠CED+∠ADE=∠CED+α,
∴∠BMC=∠CED+α+∠CEA=∠AED+α=![]() +α=
+α=![]() 。
。


科目:初中数学 来源: 题型:
【题目】我省某工艺厂为全运会设计了一款成本为每件20元得工艺品,投放市场进行试销后发现每天的销售量y(件)是售价x(元∕件)的一次函数,当售价为22元∕件时,每天销售量为780件;当售价为25元∕件时,每天的销售量为750件.
(1)求y与x的函数关系式;
(2)如果该工艺品售价最高不能超过每件30元,那么售价定为每件多少元时,工艺厂销售该工艺品每天获得的利润最大?最大利润是多少元?(利润=售价﹣成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
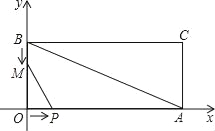
【题目】如图,在平面直角坐标系xOy中,已知矩形OACB的边OA,OB分别在x轴上和y轴上,线段OA=24,OB=12;点P从点O开始沿OA边匀速移动,点M从点B开始沿BO边匀速移动.如果点P,点M同时出发,它们移动的速度相同都是1个单位/秒,设经过x秒时(0≤x≤12),△POM的面积为y.
(1)求直线AB的解析式;
(2)求y与x的函数关系式;
(3)连接矩形的对角线AB,当x为何值时,以M、O、P为顶点的三角形等于△AOB面积的![]() ;
;
(4)当△POM的面积最大时,将△POM沿PM所在直线翻折后得到△PDM,试判断D点是否在直线AB上,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x(x-2)=x-2①与一元一次方程2x+1=2a-x②.
(1)若方程①的一个根是方程②的根,求a的值;
(2)若方程②的根不小于方程①两根中的较小根且不大于方程①两根中的较大根,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到_____元购物券,至多可得到_______元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(1)求一次函数与反比例函数的解析式;
(2)求两函数图象的另一个交点坐标;
(3)直接写出不等式;kx+b≤![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小虫从某点![]() 点处出发在一直线上来回爬行,假定向右爬行的路程记为正数,左爬行的路程为负数,爬行的路程依次为(单位:厘米):+5,-3,+10,-8,-6,+12,-11.
点处出发在一直线上来回爬行,假定向右爬行的路程记为正数,左爬行的路程为负数,爬行的路程依次为(单位:厘米):+5,-3,+10,-8,-6,+12,-11.
(1)小虫最后是否回到出发点![]() 点?如果不在,请说出小虫的位置;
点?如果不在,请说出小虫的位置;
(2)小虫离开出发点![]() 点最远时是 厘米;
点最远时是 厘米;
(3)在爬行过程中,如果每爬1厘米奖励两粒芝麻,则小虫共得多少粒芝麻?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)阅读下列材料:
(1)关于x的方程x2-3x+1=0(x≠0)方程两边同时乘以![]() 得:
得: ![]() 即
即![]() ,
, ![]() ,
,
(2)a3+b3=(a+b)(a2-ab+b2);a3-b3=(a-b)(a2+ab+b2).
根据以上材料,解答下列问题:
(1)x2-4x+1=0(x≠0),则![]() = ______ ,
= ______ , ![]() = ______ ,
= ______ , ![]() = ______ ;
= ______ ;
(2)2x2-7x+2=0(x≠0),求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程![]() .
.
(1)求证:无论k为何值,方程总有实数根.
(2)设![]() 是方程
是方程![]() 的两个根,记
的两个根,记![]() ,S的值能为2吗?若能,求出此时k的值;若不能,请说明理由.
,S的值能为2吗?若能,求出此时k的值;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com