
【题目】若D点坐标(4,3),点P是x轴正半轴上的动点,点Q是反比例函数![]() 图象上的动点,若△PDQ为等腰直角三角形,则点P的坐标是________.
图象上的动点,若△PDQ为等腰直角三角形,则点P的坐标是________.
【答案】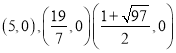
【解析】∵3×4=12,
∴点D在反比例y=![]() (x>0)图象上,
(x>0)图象上,
当QP=QD,∠PQD=90°,如图1,作QA⊥x轴于A,DH⊥x轴与H,QB⊥DH于B,

易证得△QPA≌△QDB,则BQ=QA,
设Q点坐标为(x, ![]() ),
),
∴QA=![]() ,BQ=x4,
,BQ=x4,
∴![]() =x4,解得x=6(x=2舍去),
=x4,解得x=6(x=2舍去),
∴Q点坐标为(6,2),
∴QA=2,PA=BD=32=1,
∴PQ=![]() ,
,
∴DP=![]() PQ=
PQ=![]() ,
,
在Rt△DPH中,DH=3,
∴PH=![]() ,
,
∴OP=5,
∴P点坐标为(5,0);
当DP=DQ,∠PDQ=90°,如图2,作QA⊥x轴于A,DH⊥x轴与H,QB⊥DH于B,
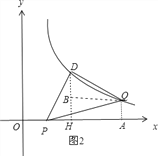
易证得△DPH≌△QDB,则BQ=DH=3,BD=PH,
∴Q点坐标为(7, ![]() ),
),
∴BD=3![]() =
=![]() ,
,
∴PH=![]() ,
,
∴OP=4![]() =
=![]() ,
,
∴P点坐标为(![]() ,0);
,0);
当PD=PQ,∠DPQ=90,如图3,作QA⊥x轴于A,DH⊥x轴与H,

易证得△DPH≌△PQA,则BQ=PA=3,PH=QA,
设PH=t,则QA=t,
∴Q点坐标为(t+7,t),
∴t(t+7)=12,解得t=![]() (t=
(t=![]() 舍去),
舍去),
∴OP=4+![]() =
=![]() ,
,
∴P点坐标为(![]() ,0).
,0).
故答案为(5,0)、(![]() ,0)、,(
,0)、,(![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(1)求一次函数与反比例函数的解析式;
(2)求两函数图象的另一个交点坐标;
(3)直接写出不等式;kx+b≤![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:锐角△ABC中,∠C=2∠B,AD是高,求证:AC+CD=BD.
线段和差,通常用截长或补短法证明,下面是甲、乙两位同学的思路,请你按他们的思路,给出一种证明.
甲:截长法,在DB上截取DE=DC,连AE,去证BE=AC;
乙:补短法,延长DC到E,使CE=CA,连接AE,去证DB=DE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程![]() .
.
(1)求证:无论k为何值,方程总有实数根.
(2)设![]() 是方程
是方程![]() 的两个根,记
的两个根,记![]() ,S的值能为2吗?若能,求出此时k的值;若不能,请说明理由.
,S的值能为2吗?若能,求出此时k的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,有一个内角是直角的三角形是直角三角形,其中直角所在的两条边叫直角边,直角所对的边叫斜边(如图①所示).数学家还发现:在一个直角三角形中,两条直角边长的平方和等于斜边长的平方。即如果一个直角三角形的两条直角边长度分别是![]() 和
和![]() ,斜边长度是
,斜边长度是![]() ,那么
,那么![]() 。
。
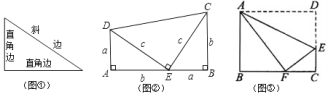
(1)直接填空:如图①,若a=3,b=4,则c= ;若![]() ,
,![]() ,则直角三角形的面积是 ______ 。
,则直角三角形的面积是 ______ 。
(2)观察图②,其中两个相同的直角三角形边AE、EB在一条直线上,请利用几何图形的之间的面积关系,试说明![]() 。
。
(3)如图③所示,折叠长方形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8,BC=10,利用上面的结论求EF的长?
查看答案和解析>>
科目:初中数学 来源: 题型:
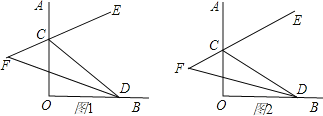
【题目】如图,∠AOB=90°,点C、D分别在射线OA、OB上,CE是∠ACD的平分线,CE的反向延长线与∠CDO的平分线交于点F.
(1)当∠OCD=50°(图1),试求∠F.
(2)当C、D在射线OA、OB上任意移动时(不与点O重合)(图2),∠F的大小是否变化?若变化,请说明理由;若不变化,求出∠F.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解下列方程: (1)x2-49=0 (2)3x2-7x=0 (3)(2x-1)2=9
(4)x2+3x-4=0 (5)(x+4)2=5(x+4) (6)x2+4x=2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题提出)
(1)如图①,已知 AB ∥CD,求证 :∠1+∠MEN+∠2=360°

(推广应用)
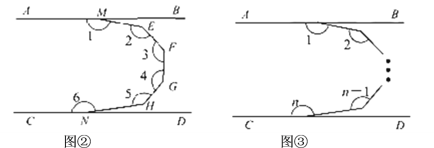
(2)如图②,已知 AB∥ CD,求∠1+∠2+∠3+∠4+∠5 +∠6的度数为___________.
如图③,已知 AB∥CD ,求∠1+∠2+∠3+∠4+∠5 +∠6+…+∠n的度数为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com