
【题目】(问题提出)
(1)如图①,已知 AB ∥CD,求证 :∠1+∠MEN+∠2=360°

(推广应用)
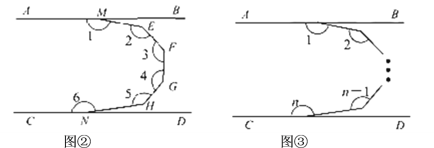
(2)如图②,已知 AB∥ CD,求∠1+∠2+∠3+∠4+∠5 +∠6的度数为___________.
如图③,已知 AB∥CD ,求∠1+∠2+∠3+∠4+∠5 +∠6+…+∠n的度数为_________.
【答案】(1)见解析,(2)![]()
【解析】
(1)过点E作EF∥CD,根据平行线的判定得出EF∥AB,根据平行线的性质得出即可;(2)如图②过E作EQ∥CD,过F作FW∥CD,过G作GR∥CD,过H作HY∥CD,根据平行线的判定得出EQ∥FW∥GR∥HY∥AB∥CD,根据平行线的性质得出即可;如图③,利用(1)(2)②发现规律,直接得到答案.
证明:(1)证明:过点E作EF∥CD,
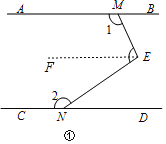
∵AB∥CD, ∴EF∥AB,
∴∠1+∠MEF=180°,
同理∠2+∠NEF=180°,
∴∠1+∠2+∠MEN =360°;
(2)如图②过E作EQ∥CD,过F作FW∥CD,过G作GR∥CD,过H作HY∥CD,
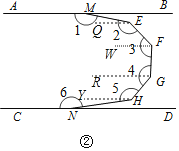
∵CD∥AB, ∴EQ∥FW∥GR∥HY∥AB∥CD,
∴∠1+∠MEQ=180°,∠QEF+∠EFW=180°,∠WFG+∠FGR=180°,
∠RGH+∠GHY=180°,∠YHN+∠6=180°,
∴∠1+∠2+∠3+∠4+∠5+∠6=5×180°=900°,
如图③,由∠1+∠2+∠MEN![]() ,
,
∠1+∠2+∠3+∠4+∠5+∠6![]() ,
,
可得:∠1+∠2+∠3+∠4+∠5+∠6+…+∠n![]() ,
,
故答案为:900°,![]() ;
;


科目:初中数学 来源: 题型:
【题目】如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE∥BD, DE∥AC , AD=2![]() , DE=2,则四边形 OCED 的面积为( )
, DE=2,则四边形 OCED 的面积为( )

A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 8
D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师请同学思考如下问题:如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗?
小敏在思考问题时,有如下思路:连接AC.

结合小敏的思路作答:
(1)若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?说明理由,参考小敏思考问题的方法解决一下问题;
(2)如图2,在(1)的条件下,若连接AC,BD.
①当AC与BD满足什么条件时,四边形EFGH是菱形,写出结论并证明;
②当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为![]() 、
、![]() ,点D是OA的中点,点P在BC边上运动,当
,点D是OA的中点,点P在BC边上运动,当![]() 是等腰三角形时,点Р的坐标为_______________.
是等腰三角形时,点Р的坐标为_______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了促进节能减排,倡导节约用电,某市将实行居民生活用电阶梯电价方案,图中折线反映了每户每月用电电费y(元)与用电量x(度)间的函数关系式.
(1)根据图象,阶梯电价方案分为三个档次,填写下表:
档次 | 第一档 | 第二档 | 第三档 |
每月用电量x(度) | 0<x≤140 |
(2)小明家某月用电120度,需交电费 元
(3)求第二档每月电费y(元)与用电量x(度)之间的函数关系式;
(4)在每月用电量超过230度时,每多用1度电要比第二档多付电费m元,小刚家某月用电290度,交电费153元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
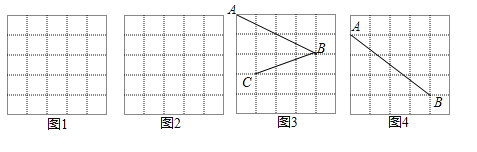
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.
(1)在图1中以格点为顶点的画一个面积为5的等腰直角三角形;
(2)在图2中以格点为顶点画一个三角形,使三角形三边长分别为2,![]()
(3)如图3,点A,B,C是格点,则∠ABC= ;
(4)在图4中画出△ABC(点C是格点),使△ABC为等腰三角形(画一个).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.
![]()
(1)请你补全这个输水管道的圆形截面;
(2)若这个输水管道有水部分的水面宽AB=16 cm,水面最深地方的高度为4 cm,求这个圆形截面的半径;
(3)在(2)的条件下,小明把一只宽12 cm的方形小木船放在修好后的圆柱形水管里,已知船高出水面13 cm,问此小船能顺利通过这个管道吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com