
【题目】如图:锐角△ABC中,∠C=2∠B,AD是高,求证:AC+CD=BD.
线段和差,通常用截长或补短法证明,下面是甲、乙两位同学的思路,请你按他们的思路,给出一种证明.
甲:截长法,在DB上截取DE=DC,连AE,去证BE=AC;
乙:补短法,延长DC到E,使CE=CA,连接AE,去证DB=DE.

【答案】见解析.
【解析】
甲:由线段垂直平分线的性质可得AE=AC,由等腰三角形的性质可得∠AEC=∠C,由外角性质可得∠B=∠BAE,可得AE=BE=AC,即可得结论;
乙:由外角性质可得∠ACB=2∠E,可得∠B=∠E,可得AB=AE,由等腰三角形的性质可得BD=DE,即可得结论.
解:甲:截长法,如图1,在DB上截取DE=DC,连AE,
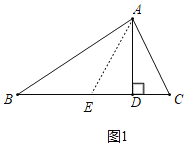
∵DE=DC,AD⊥BC,
∴AE=AC,
∴∠AEC=∠C,且∠C=2∠B,
∴∠AEC=∠B,且∠AEC=∠B+∠BAE,
∴∠B=∠BAE,
∴AE=BE=AC,
∴BD=BE+DE=AC+CD
乙:补短法,延长DC到E,使CE=CA,连接AE,
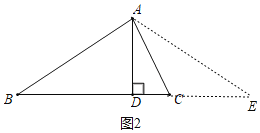
∵CE=CA,
∴∠E=∠CAE,且∠ACB=∠E+∠CAE,
∴∠ACB=2∠E,且∠ACB=2∠B,
∴∠B=∠E,
∴AB=AE,且AD⊥BC,
∴BD=DE,
∵DE=DC+CE=AC+DC,
∴BD=DC+AC.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
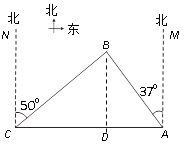
【题目】南中国海是中国固有领海,我渔政船经常在此海域执勤巡察.一天我渔政船停在小岛A北偏西37°方向的B处,观察A岛周边海域.据测算,渔政船距A岛的距离AB长为10海里.此时位于A岛正西方向C处的我渔船遭到某国军舰的袭扰,船长发现在其北偏东50°的方向上有我方渔政船,便发出紧急求救信号.渔政船接警后,立即沿BC航线以每小时30海里的速度前往救助,问渔政船大约需多少分钟能到达渔船所在的C处?
![]() (参考数据:sin37°≈0.60,cos37°≈0.80,sin50°≈0.77,cos50°≈0.64,sin53°≈0.80,cos53°≈0.60,sin40°≈0.64,cos40°≈0.77)
(参考数据:sin37°≈0.60,cos37°≈0.80,sin50°≈0.77,cos50°≈0.64,sin53°≈0.80,cos53°≈0.60,sin40°≈0.64,cos40°≈0.77)
查看答案和解析>>
科目:初中数学 来源: 题型:
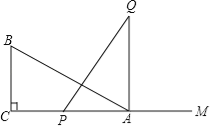
【题目】如图,有一直角三角形ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线AQ上运动,问P点运动到AC上什么位置时△ABC才能和△APQ全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
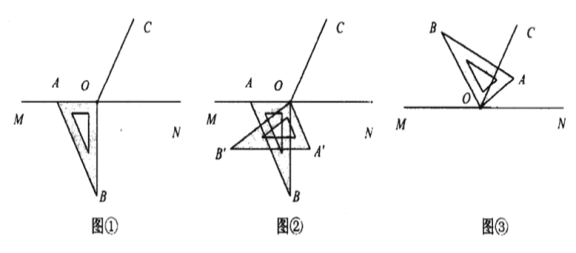
【题目】如图①,点![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作直线
作直线![]() ,使
,使![]() .将一把直角三角尺的直角顶点放在点
.将一把直角三角尺的直角顶点放在点![]() 处,一边
处,一边 ![]() 在射线
在射线![]() 上,另一边
上,另一边![]() 在直线
在直线![]() 的下方,其中
的下方,其中![]()
![]() 将图②中的三角尺沿直线
将图②中的三角尺沿直线![]() 翻折至
翻折至![]() , 求
, 求![]() 的度数;
的度数;
![]() 将图①中的三角尺绕点
将图①中的三角尺绕点![]() 按每秒
按每秒![]() 的速度沿顺时针方向旋转,旋转角为
的速度沿顺时针方向旋转,旋转角为![]() , 在旋转的过程中,在第几秒时,直线
, 在旋转的过程中,在第几秒时,直线![]() 恰好平分锐角
恰好平分锐角![]() .
.
![]() 将图①中的三角尺绕点
将图①中的三角尺绕点![]() 顺时针旋转;当点
顺时针旋转;当点![]() 点
点![]() 均在直线
均在直线![]() 上方时(如图③所示),请探究
上方时(如图③所示),请探究![]() 与
与![]() 之间的数量关系,请直接写出结论,不必写出理由.
之间的数量关系,请直接写出结论,不必写出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式:![]() ,
,![]() .给出定义如下:使等式
.给出定义如下:使等式![]() 成立的一对有理数
成立的一对有理数![]() ,
,![]() 为“共生有理数对”,记为
为“共生有理数对”,记为![]() .如:数对
.如:数对![]() ,
,![]() 都有“共生有理数对”.
都有“共生有理数对”.
(1)数对![]() ,
,![]() 中是“共生有理数对”的是 .
中是“共生有理数对”的是 .
(2)请再写出另外一对符合条件的“共生有理数对” (不能与题目中已有的重复).
(3)小丁说:“若![]() 是‘共生有理数对’,则
是‘共生有理数对’,则![]() 一定是‘共生有理数对’.”请你用(2)中写出的“共生有理数对”验证小丁的说法.
一定是‘共生有理数对’.”请你用(2)中写出的“共生有理数对”验证小丁的说法.
查看答案和解析>>
科目:初中数学 来源: 题型:
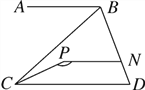
【题目】如图,已知AB∥PN∥CD.
(1)试探索∠ABC,∠BCP和∠CPN之间的数量关系,并说明理由;
(2)若∠ABC=42°,∠CPN=155°,求∠BCP的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解本校2400名学生对某次足球赛的关注程度,以利于做好教育和引导工作,随机抽取了本校内的六、七、八、九四个年级部分学生进行调查,按“各年级被抽取人数”与“关注程度”,分别绘制了条形统计图(图①)、扇形统计图(图②)和折线统计图(图③).

(1)本次共随机抽查了________名学生,根据信息补全图①中条形统计图,图②中八年级所对应扇形的圆心角的度数为________;
(2)如果把“特别关注”“一般关注”“偶尔关注”都看成关注,那么全校关注足球赛的学生大约有多少名?
(3)①根据上面的统计结果,谈谈你对该校学生对足球关注的现状的看法及建议;
②如果要了解中小学生对校园足球的关注情况,你认为应该如何进行抽样?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE∥BD, DE∥AC , AD=2![]() , DE=2,则四边形 OCED 的面积为( )
, DE=2,则四边形 OCED 的面积为( )

A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 8
D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com